最短路¶
前置知识¶
建图,BFS,贪心
目标¶
Bellman-Ford, SPFA, Dijkstra朴素和堆优化, Floyd,四个算法的代码模板
What¶
Shortest paths最短路 Finding a shortest path between two nodes of a graph is an important problem that has many practical applications. For example, a natural problem related to a road network is to calculate the shortest possible length of a route between two cities, given the lengths of the roads.
In an unweighted graph, the length of a path equals the number of its edges, and we can simply use breadth-first search to find a shortest path. However, in this chapter we focus on weighted graphs where more sophisticated algorithms are needed for finding shortest paths.
如果边权都是1,求最短路,就可以直接用BFS
Bellman–Ford algorithm,单源最短路,负权边,可判负环,不超过k边¶
发音,bellman ford
The Bellman–Ford algorithm finds shortest paths from a starting node to all nodes of the graph. The algorithm can process all kinds of graphs, provided that the graph does not contain a cycle with negative length. If the graph contains a negative cycle, the algorithm can detect this.
The algorithm keeps track of distances from the starting node to all nodes of the graph. Initially, the distance to the starting node is 0 and the distance to all other nodes in infinite. The algorithm reduces the distances by finding edges that shorten the paths until it is not possible to reduce any distance.
Let us consider how the Bellman–Ford algorithm works in the following graph:
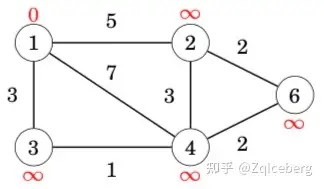
Each node of the graph is assigned a distance. Initially, the distance to the starting node is 0, and the distance to all other nodes is infinite.
The algorithm searches for edges that reduce distances. First, all edges from node 1 reduce distances:
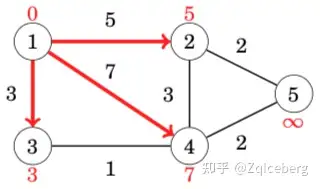
After this, edges 2 → 5 and 3 → 4 reduce distances:
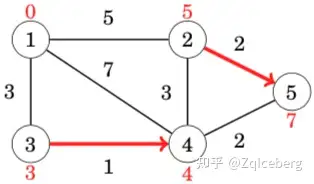
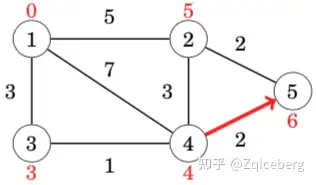
After this, no edge can reduce any distance. This means that the distances are final, and we have successfully calculated the shortest distances from the starting node to all nodes of the graph.
For example, the shortest distance 3 from node 1 to node 5 corresponds to the following path:
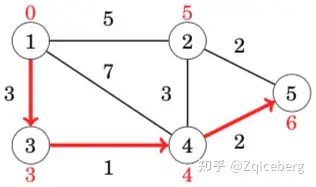
OI-Wiki的介绍,https://oi-wiki.org/graph/shortest-path/#bellman-ford-%E7%AE%97%E6%B3%95


如果最短路存在,一定存在一个不含环的最短路(思考这个事实的正确性) 边权,可正、可负。环,有零环、正环、负环。
# 题意:
从1到n的最短距离是多少,有重边,无法到达输出-1
# 思路:
跑Bellman-Ford
不需要建图,只是把所有的边存到结构体当中
循环n-1次,每一次都暴力把所有的边,进行松弛操作
在松弛操作的时候,要使用上一轮的bk[],否则会在当前这轮发生类似串联更新的现象
如果不使用备份,那么这一轮的迭代,更新后的结点,会直接影响他后面相连的结点。而实际上,后面的结点,其实不应该被他更新,因为这一轮轮不到他。
如果使用备份,后面的结点,就不会被错误的更新。
# 代码:
#include <bits/stdc++.h>
using namespace std;
struct Edge{
int a, b, w;
Edge(int _a = 0, int _b = 0, int _w = 0): a(_a), b(_b), w(_w){}
}edge[20010];
int n, m, d[2010], bk[2010];
void bellman_ford(){
memset(d, 0x3f, sizeof d);
d[1] = 0;
for (int i = 0; i < n - 1; i++){
memcpy(bk, d, sizeof bk);
for (int j = 0; j < m * 2; j++){
int a = edge[j].a, b = edge[j].b, w = edge[j].w;
d[b] = min(d[b], bk[a] + w);
}
}
}
int main(){
cin >> n >> m;
for (int i = 0; i < m * 2; i += 2){
int a, b, w;
cin >> a >> b >> w;
edge[i] = Edge(a, b, w), edge[i + 1] = Edge(b, a, w);
}
bellman_ford();
if (d[n] > 0x3f3f3f3f / 2) cout << -1 << '\n';
else cout << d[n] << '\n';
return 0;
}
// 使用vector建图,在枚举边的时候,暴力枚举所有的边
// 所有的边O(m),整体时间复杂度O(nm)
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
vector<PII> h[2010];
int n, m, d[2010], bk[2010];
void bellman_ford(){
memset(d, 0x3f, sizeof d);
d[1] = 0;
for (int i = 0; i < n - 1; i++){
memcpy(bk, d, sizeof bk);
for (int j = 0; j < n; j++) // O(m)
for (auto x : h[j]){
int a = j, b = x.first, c = x.second;
d[b] = min(d[b], bk[a] + c);
}
}
}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i++){
int a, b, c;
cin >> a >> b >> c;
h[a].push_back({b, c}); h[b].push_back({a, c});
}
bellman_ford();
if (d[n] > 0x3f3f3f3f / 2) cout << -1 << '\n';
else cout << d[n] << '\n';
return 0;
}
补充说明: 有负权回路的时候,不一定存在最短路。 如果负权回路,在最短路的路径上,那么影响。 如果负权回路,不在最短路的路径上,那么不影响。
bk[ ] 数组,在求最多不得超过 k 条边的问题时,是有用的。因为如果串联,将影响具体使用了几条边的问题。 d[n] > 0x3f3f3f3f / 2,是应为虽然结点n,从起点不可达,但是可能从相邻的点可达,相邻的点到结点n的边权是一个小的负数,那么严格写成d[n] == 0x3f3f3f3f,就不成立了。因为更新所有边的时候,d[n] 会被更新变小一点。
SPFA algorithm,队列优化的Bellman-Ford¶
发音,S-P-F-A
The SPFA algorithm (”Shortest Path Faster Algorithm”) is a variant of the Bellman–Ford algorithm, that is often more efficient than the original algorithm. The SPFA algorithm does not go through all the edges on each round, but instead, it chooses the edges to be examined in a more intelligent way.
The algorithm maintains a queue of nodes that might be used for reducing the distances. First, the algorithm adds the starting node x to the queue. Then, the algorithm always processes the first node in the queue, and when an edge a → b reduces a distance, node b is added to the queue.
The efficiency of the SPFA algorithm depends on the structure of the graph: the algorithm is often efficient, but its worst case time complexity is still *O*(*nm*)** and it is possible to create inputs that make the algorithm as slow as the original Bellman–Ford algorithm.(如果是一个网格状的图,就会卡SPFA)
OI-Wiki的介绍,https://oi-wiki.org/graph/shortest-path/#%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96spfa


# 题意:
从1到n的最短距离是多少,有重边有自环,n <= 1e5, m <= 5e5
# 思路:
bellman_ford O(nm)会爆,跑SPFA,O(m)
# 代码:
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
vector<PII> h[N];
int n, m, d[N];
bool vis[N];
void spfa(){
memset(d, 0x3f, sizeof d);
d[1] = 0;
queue<int> q;
q.push(1);
vis[1] = true;
while (!q.empty()){
int t = q.front(); q.pop();
vis[t] = false;
for (auto x : h[t]){
int a = t, b = x.first, c = x.second;
if (d[b] > d[a] + c){
d[b] = d[a] + c;
if (!vis[b]){
q.push(b);
vis[b] = true;
}
}
}
}
}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i++){
int a, b, c;
cin >> a >> b >> c;
if (a == b) continue;
h[a].push_back({b, c}); h[b].push_back({a, c});
}
spfa();
cout << d[n] << '\n';
return 0;
}
Dijkstra’s algorithm,单源最短路,边权都是正数¶
发音,迪杰斯特拉
Dijkstra’s algorithm finds shortest paths from the starting node to all nodes of the graph, like the Bellman–Ford algorithm. The benefit of Dijsktra’s algorithm is that it is more efficient and can be used for processing large graphs. However, the algorithm requires that there are no negative weight edges in the graph.(原理是基于贪心)
Like the Bellman–Ford algorithm, Dijkstra’s algorithm maintains distances to the nodes and reduces them during the search. Dijkstra’s algorithm is efficient, because it only processes each edge in the graph once, using the fact that there are no negative edges.
Let us consider how Dijkstra’s algorithm works in the following graph when the starting node is node 1:
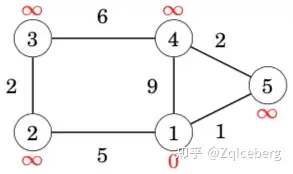
Like in the Bellman–Ford algorithm, initially the distance to the starting node is 0 and the distance to all other nodes is infinite.
At each step, Dijkstra’s algorithm selects a node that has not been processed yet and whose distance is as small as possible. The first such node is node 1 with distance 0.
When a node is selected, the algorithm goes through all edges that start at the node and reduces the distances using them:
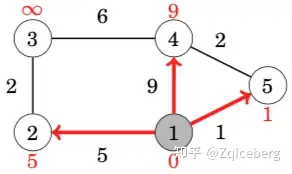
In this case, the edges from node 1 reduced the distances of nodes 2, 4 and 5, whose distances are now 5, 9 and 1. The next node to be processed is node 5 with distance 1. This reduces the distance to node 4 from 9 to 3:
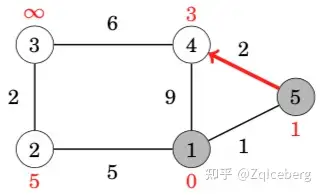
After this, the next node is node 4, which reduces the distance to node 3 to 9:
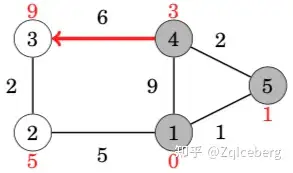
A remarkable property in Dijkstra’s algorithm is that whenever a node is selected, its distance is final. For example, at this point of the algorithm, the distances 0, 1 and 3 are the final distances to nodes 1, 5 and 4.
After this, the algorithm processes the two remaining nodes, and the final distances are as follows:
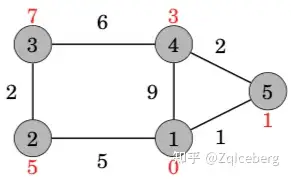
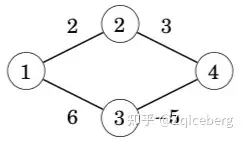
对于有负权边的图,Dijkstra是不可用的。The shortest path from node 1 to node 4 is 1 → 3 → 4 and its length is 1. However, Dijkstra’s algorithm finds the path 1 → 2 → 4 by following the minimum weight edges. The algorithm does not take into account that on the other path, the weight −5 compensates the previous large weight 6.
OI-Wiki的介绍,https://oi-wiki.org/graph/shortest-path/#dijkstra-%E7%AE%97%E6%B3%95

# 题意
求1到n的最短路径,数据范围1≤n≤2000,1≤m≤10000
# 思路
跑朴素版的Dijkstra
# 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2010, M = 2e5 + 10;
int g[N][N];
LL d[N];
bool st[N];
int n, m;
void dijkstra()
{
memset(d, 0x3f, sizeof d);
d[1] = 0;
for (int i = 0; i < n - 1; i++){
int t = -1;
for (int j = 1; j <= n; j++)
if (!st[j] && (t == -1 || d[j] < d[t]))
t = j;
st[t] = true;
for (int j = 1; j <= n; j++)
d[j] = min(d[j], d[t] + g[t][j]);
}
}
int main()
{
memset(g, 0x3f, sizeof g);
cin >> n >> m;
while (m--){
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
g[b][a] = g[a][b];
}
dijkstra();
if (d[n] == 0x3f3f3f3f) cout << -1 << '\n';
else cout << d[n] << '\n';
return 0;
}
例题,1420:Dijkastra(II) 堆优化版本
# 题意
求1到n的最短路,N≤200000,M≤400000,d <= 1e9
# 思路
堆优化版,稀疏图,O(mlogm)
the algorithm goes through all nodes of the graph
and adds for each edge at most one distance to the priority queue.
边长d <= 1e9, 需要开long long
# 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, int> PII;
const int N = 2e5 + 10;
vector<PII> h[N];
int n, m;
ll d[N];
bool vis[N];
void dijkstra(){
memset(d, 0x3f, sizeof d);
d[1] = 0ll;
priority_queue<PII> q;
q.push({0ll, 1});
while (!q.empty()){
PII t = q.top(); q.pop();
int ver = t.second;
if (vis[ver]) continue;
vis[ver] = true;
for (auto x : h[ver]){
int a = ver, b = x.second;
ll c = x.first;
if (d[b] > d[a] + c){
d[b] = d[a] + c;
q.push({-d[b], b});
}
}
}
}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i++){
int a, b, c;
cin >> a >> b >> c;
h[a].push_back({c, b}); h[b].push_back({c, a});
}
dijkstra();
cout << d[n] << '\n';
return 0;
}
Floyd–Warshall algorithm多源汇最短路,边权可正可负,但不能有负环¶
发音,弗洛伊德

邻接矩阵建图,要注意数据范围,还有图不能很大
动态规划的状态定义
f[k][x][y],表示x到y的,只以(1...k)集合中的结点为中间结点的,最短路径的长度。
状态转移方程
f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]);
压缩第一维
f[x][y] = min(f[x][y], f[x][k] + f[k][y]);
压缩的证明,https://oi-wiki.org/graph/shortest-path/#floyd-%E7%AE%97%E6%B3%95
划分阶段,
我们定义 f[k][i][j]为经过前k的节点,
从i到j所能得到的最短路径,f[k][i][j]可以从f[k-1][i][j]转移过来,即不经过第k个节点,
也可以从f[k-1][i][k]+f[k-1][k][j]转移过来,即经过第k个节点。
最优子结构:
图结构中一个显而易见的定理:最短路径的子路径仍然是最短路径 ,
这个定理显而易见,比如一条从a到e的最短路a->b->c->d->e
那么 a->b->c 一定是a到c的最短路,c->d->e一定是c到e的最短路,
反过来,如果说一条最短路必须要经过点k,那么i->k的最短路加上k->j的最短路一定是i->j 经过k的最短路,
因此,最优子结构可以保证。
无后效性:
状态f[k][i][j]由f[k-1][i][j],f[k-1][i,k] 以及f[k-1][k][j]转移过来,
很容易可以看出,f[k] 的状态完全由f[k-1]转移过来,只要我们把k放倒最外层循环中,就能保证无后效性。
动态规划的基本要素,子问题重叠性,最优子问题,无后效性,https://zhuanlan.zhihu.com/p/33162490#:~:text=Floyd%E7%AE%97%E6%B3%95%E5%8F%AA,%E4%BE%BF%E6%88%90%E4%B8%BA%E4%BA%86%E8%B4%9F%E6%97%A0%E7%A9%B7%E3%80%82
Floyd算法允许有带负权值的边,但不允许有包含带负权值的边组成的回路
这句话的意思并不是说“只要回路中存在负权值Floyd就不可以解决” 而是“组成这个回路的所有的边的权值之和如果为负,就无法解决,否则还是可以解决的”
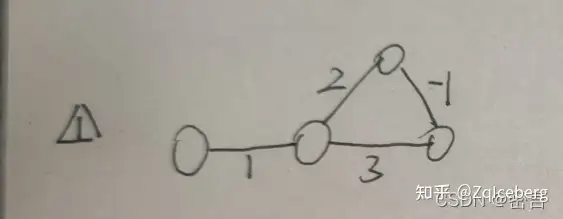

参考链接,https://blog.csdn.net/ThePythonFucker/article/details/123193579
# 题意
从1到{1...n}所有点的最短距离之和,如何有结点无法到达,输出-1。数据保证没有负环。
# 思路
从1开始跑一遍floyd,然后枚举一遍最短路径求和。如果有一个点无法到达,就输出-1
# 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int d[N][N];
int n, m;
void floyd()
{
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main()
{
cin >> n >> m;
memset(d, 0x3f, sizeof d);
while (m--){
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
d[b][a] = d[a][b];
}
floyd();
int res = -1;
for (int j = 1; j <= n; j++){
if (d[1][j] == 0x3f3f3f3f){res = -1; break;}
res = max(res, d[1][j]);
}
cout << res << '\n';
return 0;
}
输出方案¶
https://oi-wiki.org/graph/shortest-path/#%E8%BE%93%E5%87%BA%E6%96%B9%E6%A1%88

题单¶
bellman-ford, 朴素dijkstra
SPFA
堆优化dijkstra
floyd
朴素版的dijkstra
堆优化的dijkstra
spfa,堆优化的dijkstra
spfa
floyd
floyd
bellman-ford,限制了行走时间。较难
关键是构造图,用Bellman-Ford算法找出负权环,需要注意的是输入说明 USACO 2006 December Gold难度
一个套汇问题,就是通过一系列的货币交换能够到达价值增加的目的;就是类似判断有没有负权回路;基础难度
给n种货币,和m种货币汇率。问能否通过汇率是总金额增加 求正权回路,bellman-ford,基础难度
总结¶
Bellman-Ford,单源最短路,可以存在负权边,O(nm),可以判断不超过k条边 SPFA,单源最短路,可以存在负权边,是Bellman-Ford加上了一个队列优化,一般O(m),最坏O(nm) Dijkstra,单源最短路,正权边,朴素版O(n^2)适合稠密图,堆优化版本O(mlogn)适合稀疏图 Floyd,多源汇最短路,可以有负权边,但不能有负环,动态规划,O(n^3)
要能够理解算法贪心的过程,要理解松弛操作 一个算法的演变过程,为什么有了它,它有什么特点,适合什么场景
这四个算法的模板代码,都要非常熟练默写。