分层图

前置知识

最短路，dp

目标

分层图模板题

What

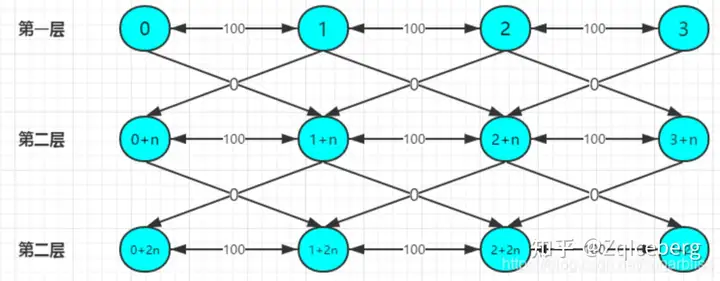
分层图最短路是指在可以进行分层图的图上解决最短路问题。分层图：可以理解为有多个平行的图。一般模型是：在一个正常的图上可以进行 k 次决策，对于每次决策，不影响图的结构，只影响目前的状态或代价。一般将决策前的状态和决策后的状态之间连接一条权值为决策代价的边，表示付出该代价后就可以转换状态了。

How

建图时，直接建成 k+1 层。（多建一条到下一层边权为0的单向边，如果走了这条边就表示用了一次机会。）

例题，飞行路线 - Virtual Judge

题意：n个城市，有m种航线，最多可以免费搭乘k种航线飞机。问这次出行的最小花费是多少

思路：a城市，到b城市，可能花费，也可能花费为0。令k层的图，表示使用了k-1次免费的机会。a->b，可能是同一层里，双向的，都有花费。也可能是从j层的a，飞到j+1层的b，花费为0。也可能从j层的b飞到j+1层的a，花费为0。也就是，每一层都有一套n个城市的分身。那么用偏移量的方法，把这些城市的二维坐标，映射到一维上。int pos(int dep, int x) return (dep-1)*n + x;。完成映射后，就跑一遍dijkstra。最后枚举一遍每一层的ed城市的距离，更新最小值

#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10, M = 1e7 + 10;
const int INF = 2e9;

int h[N], e[M], ne[M], w[M], idx;
int n, m, k;
int st, ed;
int dis[N];
bool vis[N];

struct Node
{
    int now, d;

    bool operator< (const Node& W)const
    {
        return d > W.d;
    }
};

//不同层上的点，映射到一层上
int pos(int dep, int x) 
{
    return (dep - 1) * n + x;
}

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void dijkstra()
{
    priority_queue<Node> q;

    for (int i = 1; i <= n * k; i++) dis[i] = INF;

    Node t;
    t.d = 0; t.now = st;
    q.push(t);
    dis[st] = 0;

    while (!q.empty())
    {
        Node t = q.top(); q.pop();
        int now = t.now;

        if (vis[now]) continue;
        vis[now] = true;

        for (int i = h[now]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dis[now] + w[i] < dis[j])
            {
                dis[j] = dis[now] + w[i];

                if (!vis[j])
                {
                    Node tmp;
                    tmp.d = dis[j]; tmp.now = j;
                    q.push(tmp);
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);
    k = k + 1;  //第i层，表示用了i-1次优惠

    scanf("%d%d", &st, &ed);
    st = st + 1, ed = ed + 1;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i++)
    {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        x = x + 1, y = y + 1;

        for (int j = 1; j <= k; j++)  //枚举每一层，层内部移动
        {
            int p1 = pos(j, x);
            int p2 = pos(j, y);

            add(p1, p2, z);
            add(p2, p1, z);
        }

        for (int j = 1; j < k; j++)
        {
            int p1 = pos(j, x);
            int p2 = pos(j + 1, y);  //往j+1层移动,免费一次
            add(p1, p2, 0);

            p2 = pos(j, y);
            p1 = pos(j + 1, x);      //往j+1层移动，免费一次
            add(p2, p1, 0);
        }
    }

    dijkstra();

    int ans = INF;
    for (int i = 1; i <= k; i++)
        ans = min(ans, dis[pos(i, ed)]); //每一层的ed，哪个dis最小

    printf("%d\n", ans);

    return 0;
}

总结

相当于把每个结点拆分成了 k+1 个结点，每个新结点代表使用不同多次免费通行后到达的原图结点。换句话说，就是每个结点 ui 表示使用 i 次免费通行权限后到达 u 结点。【拆点】是一种图论建模思想，用来处理点权或者点的流量限制的问题，比如网络流、分层图。

上面示范代码，是建图的时候直接拆成了k+1层。分层图，还有一种代码模板，就是使用dp，直接多开一维，记录机会信息。

// 我们把dis数组和vis数组多开一维记录k次机会的信息。

// dis[i][j] 代表到达 i 用了 j 次免费机会的最小花费.
// vis[i][j] 代表到达 i 用了 j 次免费机会的情况是否出现过.

// 状态转移方程
// 不使用机会 
dis[v][c] = min(min，dis[now][c] + edge[i].w);
// 使用机会 
dis[v][c+1] = min(dis[v][c+1]，dis[now][c]);

// 提问，请把《飞行路线》用dp思想，实现一遍，请实践

参考

分层图最短路--最通俗易懂的讲解_分层最短路_sugarbliss的博客-CSDN博客 https://oi-wiki.org/graph/node/