最大公约数¶
greatest common divisor,gcd¶
最大公因数(英语:highest common factor,hcf),也称最大公约数(英语:greatest common divisor,gcd),是指能够整除多个非零整数的最大正整数。例如8和12的最大公因数为4。
最大公约数的值至少为1,例如\(gcd(3, 7) =1\)
最大公约数的值最大为该组整数中绝对值最小的绝对值,例如\(gcd(3, 9) = 3\),\(gcd(-3, 9)=3\)
两个整数的最大公约数可用于计算两数的最小公倍数,或分数化简成最简分数。
\(gcd(a, b) \times lcm(a, b) = a \times b\)
求最大公约数的方法¶
求两个整数最大公约数的主要方法:
- 列举法:分别列出两个证书的所有约数,找出最大的公约数。
- 短除法:两数除以共同的质因子,直到两数互质时,所有除数的乘积就是最大公约数。
- 质因子分解:分别列出两个整数的质因子分解,计算共同项的乘积。
- 欧几里得算法:\(gcd(a, b) = gcd(b,a \bmod b)\) ,即 \(gcd(a, b) = gcd(b,a \% b)\)
质因子分解法¶
例如计算48和180的最大公约数。首先对两个数进行质因子分解:
\(48 = 2 \times 2 \times 2 \times 2 \times 3\)
\(180=2\times2\times3\times3\times5\)
他们之中的共同元素是两个2和一个3:

最大公约数gcd \(=2\times2\times3=12\)
最小公倍数lcm \(=2\times2\times(2\times2\times3)\times3\times5=720\)
欧几里得算法¶


// 最大公约数
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
// 最小公倍数
lcm = a * b / gcd(a, b);
实际上,不能这样写代码,会溢出!
lcm = a / gcd(a, b) * b;

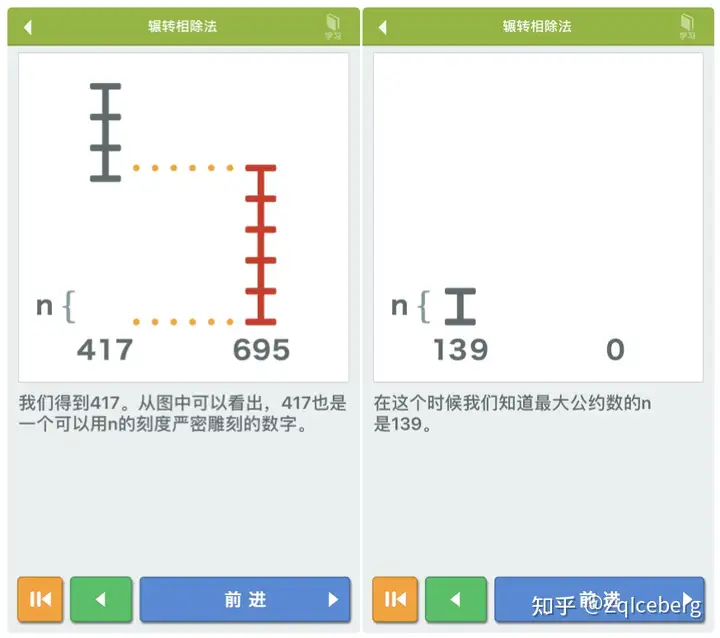
时间复杂度¶
欧几里得算法的时间效率如何呢?下面我们证明,在输入为两个长为 n 的二进制整数时,欧几里得算法的时间复杂度为 \(O(n)\)。
在默认 a,b 同阶的情况下,时间复杂度为 \(O(logmax(a, b))\)。
证明:
当我们求 \(gcd(a,b)\) 的时候,会遇到两种情况:
如果 \(a<b\),\(gcd(a, b) = gcd(b, a)\)
如果 \(a > b\),\(gcd(a, b) = gcd(b, a \bmod b)\),对 \(a\) 取模会让 \(a\) 至少折半。这意味着,这一过程至多发生 \(O(loga)\) 次
第一种情况发生后一定会发生第二种情况,因此第一种情况的发生次数一定 不多于 第二种情况的发生次数。
从而我们最多递归 \(O(n)\) 次就可以得出结果。
gcd 的等价变形¶
1¶
\(gcd(a, 0) = a\)
\(gcd(a, a) = a\)
2¶
\(gcd(a, b)=gcd(b, a \bmod b)\),其中 \(a \bmod b = a - b \cdot \lfloor \frac{a}{b} \rfloor\)
3¶
\(gcd(a, b)=gcd(a - b, b) | a > b\) (辗转相减法,更相减损术)
\(gcd(a, b)=gcd(a, b-a) | b > a\)
4¶
\(gcd(a, b) = gcd(a, b - a*k)\),只要减的是 a 的倍数,都一样。
非常适合用来:
- 化简表达式
- 化简区间
- 简化构造
- 推出不变量
5¶
多元化
\(gcd(a, b, c) = gcd(a, gcd(b, c))\)
\(gcd(a, b, c) = gcd(a - b, b - c, c)\)
6¶
\(gcd(a, b, c)=gcd(a, gcd(b-a, c-a))\)
这由 \(gcd(a, b)=gcd(a, b-a)\) 推广而来。
更多的:
\(gcd(a, b, c,d)=gcd(a, gcd(b-a, c-a, d - a))\)
7¶
所有 \(gcd(a, b)\) 的值,一定是 \(|a - b|\) 的因数
这条经常用于:
- 判断两个数能否互相变成
- 判断能否达到某个目标 (mod 性质)
- 经典水壶问题 / 数学构造题
例如:
只能向两个杯子倒水,容量 A,B 那么你只能凑出:gcd(A,B) 的倍数。
gcd 与差分¶
\(gcd(a₁, a₂, ... , aₙ) = gcd(a₁, a₂ - a₁, a₃ - a₂, ...)\)
一组数的 gcd,与它们“差分数组”的 gcd 是一样的。
很多题目:
- 只变化了某一个位置
- 或者区间整体 +k 或 -k
- 或者需要求数段的 gcd
差分可以把问题 从“求多个值的 gcd” → “求差分值的 gcd” 而差分值通常更小、更规律、能用前缀。
典型例题 1(常考)¶
给你一个数组,q 次修改,每次把某个区间 +k,问整个数组的 gcd 是否改变?
解决方法:
- 加 k 后,数组整体结构变化不大
- 但差分数组几乎不变(只有两个点变化)
你只需维护:
这是 CF 1400 常客。
典型例题 2(CF 常考)¶
给你一组 a[1…n],问有多少对 (i,j) 满足 gcd(a[i…j]) = x?
思路:
- gcd(a[l..r]) = gcd(a[l], 差分部分)
- 差分不变时 gcd 不变
- 一旦差分出现 <x 或跳跃,区间终止
差分数组是整道题的关键。
gcd 的“区间不变性”¶
如果区间整体 +k 或 -k,不会改变该区间的 gcd。
\(gcd(a[l], a[l+1], ..., a[r]) = gcd(a[l]+k,a[l+1]+k, ..., a[r]+k)\)
因为 :
\(gcd(x, y) = gcd(x, y - x) = gcd(x+k, (y+k)-(x+k))\)
写成区间就是:
整体平移不影响 gcd,但对单点修改会影响
这是许多动态查询问题的基础。
P13014 [GESP202506 五级] 最大公因数¶
for (i = 1...n) 多次询问\(gcd(a_1+i,a_2+i+...,a_n+i)\)的值。
我们可以每次for一遍,求一遍gcd,这样整体的时间复杂度是\(O(n^2 \cdot loga_i)\)
但我们利用上面这个性质的推广,则可以\(O(n \cdot loga_i)\)内解决问题。
\(gcd(a_1+i,a_2+i+...,a_n+i)\)
\(=gcd(a_1+i,(a_2+i)-(a_1+i),...,(a_n+i)-(a_1-i)\)
\(=gcd(a_1+i,a_2-a_1,...,a_n-a_1)\)
\(=gcd(a_1+i,\underline{gcd(a_2-a_1,...,a_n-a_1)})\)
这样,预处理出来后面部分的值,然后每次for循环,只需要\(O(1)\)求解
典型例题 1:区间加法 + gcd 查询(超经典)¶
给定数组,支持:
- 区间加 k
- 查询某段的 gcd
做法:
- 原数组做差分
- 区间加法只改变 diff[l] 和 diff[r+1]
- 整段 +k 不影响整个区间的 gcd
典型例题 2:判断能否让所有数相等(AtCoder ARC)¶
你只能操作:
- 对某个数 +g 或 -g(g 固定)
最后要所有数相同。
根据区间不变性:
性质-交换律¶
\(gcd(a, b) = gcd(b, a)\)
性质-结合律¶
\(gcd(a, gcd(b, c)) = gcd(gcd(a, b), c)\)
性质-分配律¶
两个整数的最大公约数和最小公倍数中存在分配率。
\(gcd(a, lcm(b,c))=lcm(gcd(a,b),gcd(a,c))\)
\(lcm(a,gcd(b,c))=gcd(lcm(a,b),lcm(a,c))\)