表达式树

前置知识

二叉树

目标

掌握表达式树代码模板

What

二叉树是表达式处理的常用工具。例如，表达式 a+b∗(c−d)−e/f

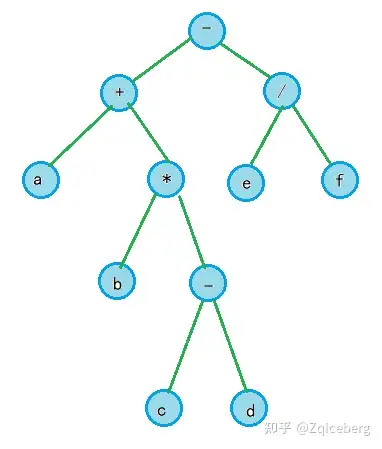
其中，每个非叶子结点表示一个运算符，

左子树是第一个运算数对应的表达式，

而右子树则是第二个运算数对应的表达式。

如何给一个表达式简历表达式树呢？

方法有很多，这里只介绍一种：找到“最后计算”的运算符（它是整颗表达式树的根），然后递归处理。

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int lch[N], rch[N], idx, root;
char op[N], s[N];

int build_tree(char *s, int x, int y){
    int c1 = -1, c2 = -1, p = 0;
    int u;

    if (y - x == 1){   // 只有一个字符了 
        u = ++idx;
        lch[u] = rch[u] = -1;
        op[u] = s[x];
        return u;
    }

    for (int i = x; i < y; i++){
        if (s[i] == '(') p++;
        if (s[i] == ')') p--;
        if (s[i] == '+' || s[i] == '-')
            if (!p) c1 = i;
        if (s[i] == '*' || s[i] == '/')
            if (!p) c2 = i;
    }

    // 找不到括号外的加减，就用乘除
    if (c1 < 0) c1 = c2;
    // 整个表达式被一对括号括起来，往里缩一位 
    if (c1 < 0) return build_tree(s, x + 1, y - 1);

    u = ++idx;
    lch[u] = build_tree(s, x, c1);
    rch[u] = build_tree(s, c1 + 1, y);
    op[u] = s[c1];

    return u;
}

void in_order(int u){
    if (lch[u] == -1 && rch[u] == -1){
        cout << op[u];
        return ;
    }

    in_order(lch[u]);
    cout << op[u];
    in_order(rch[u]);
}

void pre_order(int u){
    if (lch[u] == -1 && rch[u] == -1){
        cout << op[u];
        return ;
    }

    cout << op[u];
    pre_order(lch[u]);
    pre_order(rch[u]);
}

int main(){
    scanf("%s", s);
    root = build_tree(s, 0, strlen(s));

    in_order(root);
    puts("");
    pre_order(root);

    return 0;
}

/*
a+b*(c-d)-e/f
*/

上述代码是如何寻找“最后一个运算符”的呢？

代码用了一个变量 p，只有当 p=0 时才考虑这个运算符。为什么呢？

因为括号里的运算符一定不是最后计算的，应当忽略。

例如，(a+b)*c 中虽然有一个加号，但却是在括号里的，实际上比它优先级高的乘号才是最后计算的。

由于加减和乘除号都是左结合的，最后一个运算符才是最后计算的，所以用两个变量 c1 和 c2 分别记录“最右”出现的加减号和乘除号。

再接下来的代码就不难理解了：

如果括号外有加减号，它们肯定最后计算；

但如果没有加减号，就需要考虑乘除号（if(c1 < 0) c1 = c2）；

如果全都没有，说明整个表达式外面被一对括号括起来，把它去掉后递归调用。

这样，就找到了最后计算的运算符 s[c1]，它的左子树是区间 [x, c1]，右子树是区间 [c1+1, y]。

总结

掌握经典例题的代码

参考

紫书