[NOIP2002 提高组] T1均分纸牌

[NOIP2002 提高组] 均分纸牌

标签：贪心、递归、递推

分析：

n个纸堆，分别是a1, a2, a3, ... , an，问最少移动几次，可以让n个纸堆上的牌数一样多。

设 a 表示平均纸牌数，也就是移动的目标状态，都达到 a 就和平了。

      x1         x2         x3         x4
a1 ---> a2 ---> a3 ---> a4 ---> a5

这里xi，表示的是移动牌数的相对个数，可能是正的，也可能是负的。
正的就是从a1移动到a2，负的就是从a2移动到a1

有了这个分析过程，我们可以依次的，移动牌数，得到下面的方程

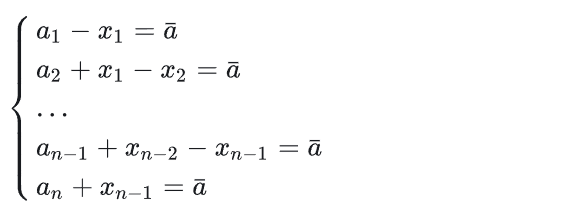
如何构造这个移动的顺序？

如果是 0 0 3， 这里不能从左开始移动，会出现移动出负数的情况
如果是 0 0 0 3 2，最佳移动方案，也并不是从最多的3开始分的，而是从2开始分的

用归纳的方法，构造这个分牌的顺序
      x1
a1 ---> [a2 a3 ... an]
假设，[a2...an]是已经均分好的，从a1分牌到a2，分的牌x1，有三种情况：
x1 = 0，不用移动
x1 > 0，从a1移动牌给a2
x1 < 0，先操作[a2...an]是他们先合法化，让a2保持可以给出去牌的状态，然后再把牌分给a1

以上，就用归纳法，构造出来了分牌的顺序

在具体求解的过程中，利用上面的方程，递推求解，当 xi 非零的时候，就需要发生一次移动牌的行为

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int a[N], n;

int main()
{
    cin >> n;

    int sum = 0;
    for (int i = 1; i <= n; i++){
        cin >> a[i];
        sum += a[i];
    }

    int ave = sum / n;
    int cnt = 0, x = 0;
    for (int i = 1; i < n; i++){
        x = a[i] - ave + x;
        if (x) cnt++;
    }

    cout << cnt << '\n';

    return 0;
}