NOIP2018普及组初赛完善程序第2题《双向链表》¶

此题在NOIP2018普及组和提高组初赛同时出现，题号分别为：

NOIP2018普及组初赛完善程序第二题 NOIP2018提高组初赛完善程序第一题

题面如下：

//这个代码是我自己写的，没有完全照搬
#include <iostream>
#include <fstream>

using namespace std;

const int N = 1e5 + 10;

int n;
int L[N], R[N], a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        a[x] = i;              // 第一空
    }

    for (int i = 1; i <= n; i++) 
    {
        R[i] = i + 1;          // 第二空
        L[i] = i - 1;
    }

    for (int i = 1; i <= n; i++) 
    {
        L[R[a[i]]] = L[a[i]];  // 第三空
        R[L[a[i]]] = R[a[i]];  // 第四空
    }

    for (int i = 1; i <= n; i++)
    {
        cout << R[i] << ' ' ;  // 第五空
    }
    puts("");

    return 0;
}

网上有很多关于初赛的答案和部分题解，也有此题的解答，讲的最深刻的就是说第三四空是基本的双向链表删除操作（就好像这样一讲，然后我就会填了），还有的解答是按照对称性填空（就好像这样一讲，然后我就会做题了）。这些我看了之后，觉得貌似懂了，但是坐下来一看，还是不懂这个双向链表怎么解决题干的要求。

题干：第i个位置之后，第一个比Pi值更大的位置，如果不存在，输出n+1

这里有一个关键点要想对，填对。

a[x] = i;

用下标作为数组的值，这种用法，在桶排里用过。这样搞一下的作用是，构造了单调性。

如果这点没想出来，写成了a[i] = x，那就妥妥拐没影了。

有了单调性之后，进行从小到大删数，当某个数被删时，链表中不存在比它小的数 （不存在比它小的数，后面单调递增的，R[i]不就找到了第一个比Pi值大的位置了嘛）

我为了理解代码，输出了中间过程。

        cout << "a[ ] ";
    for (int i = 0; i < 7; i++) printf("%3d ", a[i]);
    cout << "  输入的值在序列中的位置"; 
    puts(""); 
    cout << "结点";
    for (int i = 0; i < 7; i++) printf("%4d", i);
        cout << "   输入的值"; 
    puts("");
    cout << "L[ ] ";
    for (int i = 0; i < 7; i++) printf("%3d ", L[i]);
    puts("");
    cout << "R[ ] ";
    for (int i = 0; i < 7; i++) printf("%3d ", R[i]);
    puts("");
    puts("");

输入：

5
1 5 4 2 3

中间过程如下，可以仔细看一下这张图

画图解释一下，就是如下：

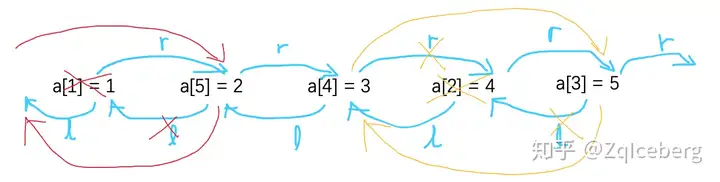
文字解释一下，就是如下：

讨论一下一般情况。当删除第2小的数时，即“2”。a[ ]数组中，a[2] = 4，记录的是数字2在原序列里，第4个出现。删除这个结点，R[4]=5，这个代表了 第4个位置后比P4值大的第一个位置是5。然后，更新第4个结点后继的前驱L[R[4]] = L[4]，更新第4个结点前驱的后继R[L[4]] = R[4]。

最后，复习一下双向链表的模板

//先搞定idx的前驱和后继。再搞定后结点的前驱，最后解决前结点的后继
void insert(int k, int x) 
{
    e[idx] = x;
    l[idx] = k;      //idx的前驱 
    r[idx] = r[k];   //idx的后继 
    l[r[k]] = idx;   //后结点的前驱 
    r[k] = idx;      //前结点的后继 
    idx++;
}

void remove(int k)
{
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

感谢大佬。

NOIP2018普及组初赛 完善程序 第2题《双向链表》¶

NOIP2018普及组初赛完善程序第2题《双向链表》¶