NOIP2014普及组初赛 完善程序 第2题《最大子矩阵》

此题在NOIP2014普及组和提高组初赛同时出现，题号分别为：

NOIP2014普及组初赛完善程序 第二题 NOIP2014提高组初赛完善程序 第二题

题面如下：

—————————————————————————

试题给的代码，不是很方便阅读和理解，重新打一遍

#include <iostream>
#include <fstream>

using namespace std;

const int N  = 100;

int matrix[N + 1][N + 1], rowsum[N + 1][N + 1];
int m, n, i, j, first, last, area, ans;

int main()
{
    freopen("zijuzhen.in", "r", stdin);
    cin >> m >> n;

    for (i = 1; i <= m; i++)
        for (j = 1; j <= n; j++)
            cin >> matrix[i][j];

    ans = matrix[1][1];                          // 左上角第一个点 
    for (i = 1; i <= m; i++) rowsum[i][0] = 0;   //  原题这个地方有换行，造成阅读诱导 

    for (i = 1; i <= m; i++)
        for (j = 1; j <= n; j++)
            rowsum[i][j] = rowsum[i][j - 1] + matrix[i][j]; //每一行做一个前缀和

    for (first = 1; first <= n; first++)           //n列，从第一列开始 
        for (last = first; last <= n; last++)  //先是列的维度 
        {
            area = 0;
            for (i = 1; i <= m; i++)      //再是行的维度，m行                       
            {
                area += rowsum[i][last] - rowsum[i][first - 1];   
                                      //ans打擂台，更新 
                                if (area > ans) ans = area;
                                     //上半部分的子矩阵和，如果是负数，清零，重头再来  
                if (area < 0) area = 0;                     
            }
        } 

    cout << ans << endl;    

    return 0;
}

注释：代码的理解，都写在了注释里，是可以帮助理解的。然后，带一组测试数据，跑一下，深入理解一下实现过程。

//zijuzhen.in
3 3
-1 1 1
1 0 0
-1 1 -1

设置debug断点

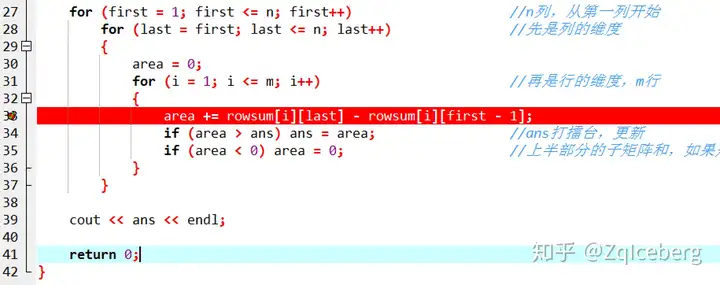
调试添加查看

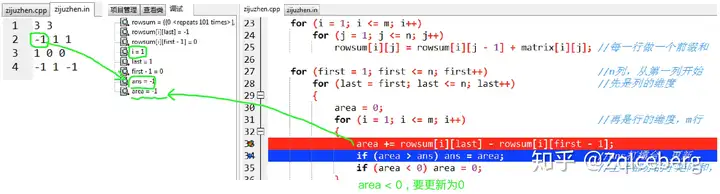
first = 1, last = 1, area += rowsum[i][last] - rowsum[i][first - 1] 。当i = 1，area代表了左上角-1的子矩阵

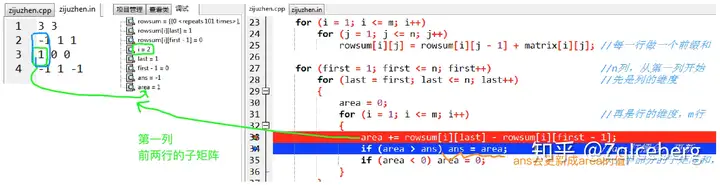
first = 1, last = 1, area += rowsum[i][last] - rowsum[i][first - 1] 。当i = 2，因为area在前一个循环被置0了，此时area代表了第一列第二行 1的子矩阵。（前面的子矩阵和，如果是负数，清零，重头再来）

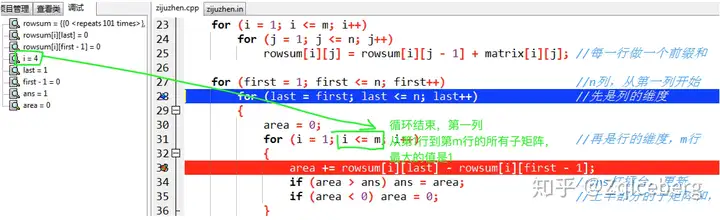
循环结束，第一列从第1行到第m行的所有子矩阵，最大的值是1

上面的执行过程符合预期

————————————————————————————————————————

这道题，是一个利用行的前缀和，求子矩阵，模板如下(惯例要感谢大佬)

s[i] = a[1] + a[2] + ... + a[i];
a[L] + ... + a[R] = s[R] - s[L - 1];

求子矩阵和的方法，还有另外的思路，如下图（利用，容斥原理）

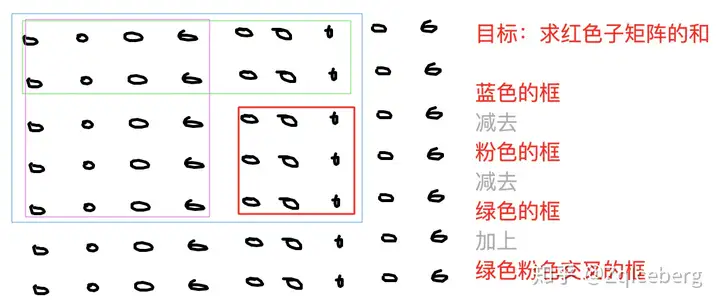
ps：初赛在即，你想了解哪些NOIP初赛题目的题解，可以留言哇