NOIP2012普及组初赛 问题求解 第2题 《排列》

Keywords: 排列组合，环

第一种方法：

大陆选手，排成一个环，共有 5!/5 种方案。对于每一种方案，都有 5 个空，让港澳选手插进去，有 5! 种插法。得到5!/5*5! = 2880

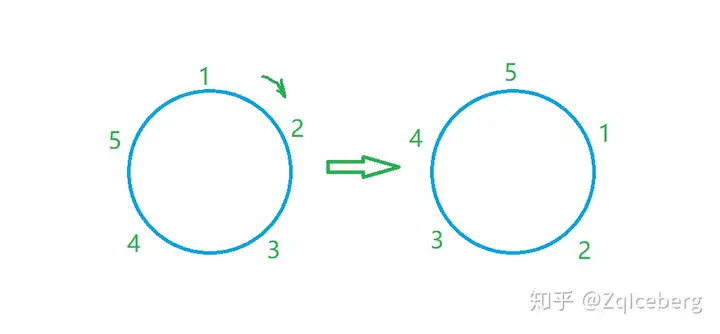
为什么5!/5，要除以5呢？因为5个选手形成一个方案后，就是形成一个环后，可以旋转得到同样的方案，每转一格得到另外一个方案，但是排序未变，也就是得到一个复本。如下图，每一种环都有5个存在。每一种环都有5个存在。所有得到的5!要除以5，这样才能不重不漏。

第二种方法：

第二种方法的计算公式是，5!*5!/5

5! * 5! 可以理解为5个位置5个位置，全排列。排好之后，从题意出发，“每个选手左边的选手相同，视为同一方案”，也就是说，一个方案内，一个大陆一个港澳为一对，一共有5对，可以旋转(5-1)次，也就存在另外4个复本。换句话说，每一种方案存在5份，需要最后除以5，保证不重。