NOIP2011普及组 T4 表达式的值

0.前言

1. 先具备表达式树的建树基础
2. 这道题目正解是用一个符号栈、一个数字栈进行模拟，可以使用模板代码实现
3. 更为重要的是思考这道题目，如何建树，跑递归，做树形dp，实现，这时会发现只有80pts
4. 有两个点是TLE，T在了建树的过程时间复杂度是O(n^2)，这个时候，搞一下笛卡尔树，O(n)时间复杂度建树
5. 更为重点的是，往上的题解有很多，有份研究报告，值得我们学习，分享在这里

1.基础知识，表达式树，紫书P353

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int lch[N], rch[N], idx;
char op[N];
char s[N];
int root;

int build(char *s, int x, int y){
    int c1 = -1, c2 = -1, p = 0;
    int u;

    if (y - x == 1){
        u = ++idx;
        lch[u] = rch[u] = 0, op[u] = s[x];
        return u;      //返回结点编号
    } 

    for (int i = x; i < y; i++){
        if (s[i] == '(') p++;
        if (s[i] == ')') p--;
        if (s[i] == '+' || s[i] == '-')
            if (!p) c1 = i;
        if (s[i] == '*' || s[i] == '/')
            if (!p) c2 = i;
    }

    if (c1 < 0) c1 = c2;
    if (c1 < 0) return build(s, x + 1, y - 1);

    u = ++idx;
    lch[u] = build(s, x, c1);
    rch[u] = build(s, c1 + 1, y);
    op[u] = s[c1];

    return u;
}

void dfs(int u){
    if (lch[u] == 0 && rch[u] == 0){
        cout << op[u];
        return ;
    }

    dfs(lch[u]);
    cout << op[u];
    dfs(rch[u]);
}

int dfs2(int u){
    if (lch[u] == 0 && rch[u] == 0){
        return op[u] - '0';
    }

    int a = dfs2(lch[u]);
    int b = dfs2(rch[u]);

    if (op[u] == '+') return a + b;
    if (op[u] == '-') return a - b;
    if (op[u] == '*') return a * b;
    if (op[u] == '/') return a / b;
}

int main(){
    scanf("%s", s);

    root = build(s, 0, strlen(s));
    //dfs(root);
    cout << dfs2(root) << '\n';

    return 0;
}

// 用这个代码，我们可以学习如何建树，适用这种表达式的题目
// 熟练使用递归

2.正解，一个符号栈，一个数字栈

#include <bits/stdc++.h>

using namespace std;

const int mod = 10007;

stack<vector<int> > num;
stack<char> op;

int n;
string s;

void eval(){
    vector<int> b = num.top(); num.pop();
    vector<int> a = num.top(); num.pop();
    char c = op.top(); op.pop();

    if (c == '*') num.push({(a[0]*b[0] + a[0]*b[1] + a[1]*b[0])%mod, a[1]*b[1]%mod});
    else num.push({a[0]*b[0]%mod, (a[0]*b[1] + a[1]*b[0] + a[1]*b[1])%mod});
}

int main(){
    map<char, int> pr;
    pr['('] = 0, pr['+'] = 1, pr['*'] = 2;

    cin >> n >> s;
    num.push({1, 1});
    for (int i = 0; i < n; i++){
        char c = s[i];
        if (c == '('){
            op.push(c);
        }
        else if (c == ')'){
            while (op.top() != '(') eval();
            op.pop();
        }
        else{
            while (op.size() && pr[op.top()] >= pr[c]) eval();
            num.push({1, 1});
            op.push(c);
        }
    }

    while (op.size()) eval();

    cout << num.top()[0] << '\n';

    return 0;
}

//  这个代码中，符号优先级的表示，eval()函数的写法，是通用的

3.开始研究建树，做树形dp

// 80pts

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10, mod = 10007;

int lch[N], rch[N], idx;
char op[N];
char s[N];

int root, n;

int build(char *s, int x, int y){
    int c1 = -1, c2 = -1, p = 0;
    int u;

    if (y - x == 0){
        u = ++idx;
        lch[u] = rch[u] = -1;
        return u;      //返回结点编号
    } 

    for (int i = x; i < y; i++){
        if (s[i] == '(') p++;
        if (s[i] == ')') p--;
        if (s[i] == '+' || s[i] == '-')
            if (!p) c1 = i;
        if (s[i] == '*' || s[i] == '/')
            if (!p) c2 = i;
    }

    if (c1 < 0) c1 = c2;
    if (c1 < 0) return build(s, x + 1, y - 1);

    u = ++idx;
    lch[u] = build(s, x, c1);
    rch[u] = build(s, c1 + 1, y);
    op[u] = s[c1];

    return u;
}

void dfs(int u){
    if (lch[u] == 0 && rch[u] == 0){
        cout << op[u];
        return ;
    }

    dfs(lch[u]);
    cout << op[u];
    dfs(rch[u]);
}

vector<int> dfs2(int u){
    if (lch[u] == -1 && rch[u] == -1){
        return {1, 1};
    }

    vector<int> a = dfs2(lch[u]);
    vector<int> b = dfs2(rch[u]);

    if (op[u] == '+') return {a[0]*b[0]%mod, (a[0]*b[1] + a[1]*b[0] + a[1]*b[1])%mod};
    if (op[u] == '*') return {(a[0]*b[0] + a[0]*b[1] + a[1]*b[0])%mod, a[1]*b[1]%mod};
}

int main(){
    scanf("%d", &n);
    getchar();
    scanf("%s", s);

    root = build(s, 0, n);
    //dfs(root);
    vector<int> ret = dfs2(root);
    cout << ret[0] << '\n';

    return 0;
}

// vector<int> dfs2(int u)，这个函数返回传递的是[0的方案数, 1的方案数]
// TLE在哪了呢？ 传递vector会耗时吗

// 建树的过程是o(n^2)的，80pts

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10, mod = 10007;

int lch[N], rch[N], idx;
char op[N];
char s[N];
int f[N][2];

int root, n;

int build(char *s, int x, int y){
    int c1 = -1, c2 = -1, p = 0;
    int u;

    if (y - x == 0){
        u = ++idx;
        lch[u] = rch[u] = -1;
        return u;      //返回结点编号
    } 

    for (int i = x; i < y; i++){
        if (s[i] == '(') p++;
        if (s[i] == ')') p--;
        if (s[i] == '+' || s[i] == '-')
            if (!p) c1 = i;
        if (s[i] == '*' || s[i] == '/')
            if (!p) c2 = i;

        if (!p && (c1 != -1 || c2 != -1)) break;
    }

    if (c1 < 0) c1 = c2;
    if (c1 < 0) return build(s, x + 1, y - 1);

    u = ++idx;
    lch[u] = build(s, x, c1);
    rch[u] = build(s, c1 + 1, y);
    op[u] = s[c1];

    return u;
}

void dfs(int u){
    if (lch[u] == 0 && rch[u] == 0){
        cout << op[u];
        return ;
    }

    dfs(lch[u]);
    cout << op[u];
    dfs(rch[u]);
}

void dfs2(int u){
    if (lch[u] == -1 && rch[u] == -1){
        f[u][0] = f[u][1] = 1;
        return ;
    }

    int a = lch[u], b = rch[u];

    dfs2(a);
    dfs2(b);

    if (op[u] == '+'){
        f[u][0] = f[a][0]*f[b][0]%mod;
        f[u][1] = (f[a][0]*f[b][1] + f[a][1]*f[b][0] + f[a][1]*f[b][1])%mod;
    }

    if (op[u] == '*'){
        f[u][0] = (f[a][0]*f[b][0] + f[a][0]*f[b][1] + f[a][1]*f[b][0])%mod;
        f[u][1] = f[a][1]*f[b][1]%mod;
    }

    return ;
}

int main(){
    freopen("P1310_2.in", "r", stdin);
    scanf("%d", &n);
    getchar();
    scanf("%s", s);

    root = build(s, 0, n);
    //dfs2(root);
    //cout << f[root][0] << '\n';

    return 0;
}

// void dfs2(int u) 改成了void类型，用f[N][2]来维护方案数
// 依然超时，研究发现是因为建树的过程dfs() 每一次执行都是O(n)的，n个点，O(n^2)

4.笛卡尔树，建树O(n)

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10, mod = 10007;

struct node{
    int lch, rch;
    char op;
}tree[N * 2];

char s[N];
int f[N][2], w[N], idx, n, root;
int st[N], k, top = -1;

void build(){
    int p = 0; //维护由多少个括号包围
    for (int i = 1; i <= n; i++){
        if (s[i] == '(') p++;
        if (s[i] == ')') p--;
        if (s[i] == '+'){
            w[++idx] = p * 2 + 1;    // 维护优先级
            tree[idx].op = s[i];
        }
        if (s[i] == '*'){
            w[++idx] = p * 2 + 2;
            tree[idx].op = s[i];
        }
    }

    // 笛卡尔建树模板
    for (int i = 1; i <= idx; i++){
        k = top;
        while (k >= 0 && w[st[k]] > w[i]) k--;
        if (k != -1) tree[st[k]].rch = i;
        if (k < top) tree[i].lch = st[k + 1];
        st[++k] = i;
        top = k;
    }

    root = st[0];
}

void dfs(int u){
    if (u == 0) return ;

    int a = tree[u].lch, b = tree[u].rch;
    char op = tree[u].op;

    if (a != -1) dfs(a); 
    if (b != -1) dfs(b);

    if (op == '+'){
        f[u][0] = f[a][0]*f[b][0]%mod;
        f[u][1] = (f[a][0]*f[b][1] + f[a][1]*f[b][0] + f[a][1]*f[b][1])%mod;
    }

    if (op == '*'){
        f[u][0] = (f[a][0]*f[b][0] + f[a][0]*f[b][1] + f[a][1]*f[b][0])%mod;
        f[u][1] = f[a][1]*f[b][1]%mod;
    }

    return ;
}

int main(){
    //freopen("P1310_2.in", "r", stdin);
    scanf("%d", &n);
    getchar();
    scanf("%s", s + 1);

    build();

    f[0][0] = f[0][1] = 1;
    dfs(root);
    cout << f[root][0] << '\n';

    return 0;
}

// 这样就可以AC了

5.分享一个特别有启发的研究报告

NOIP2011Junior表达式的值(非题解方法) - 百度文库

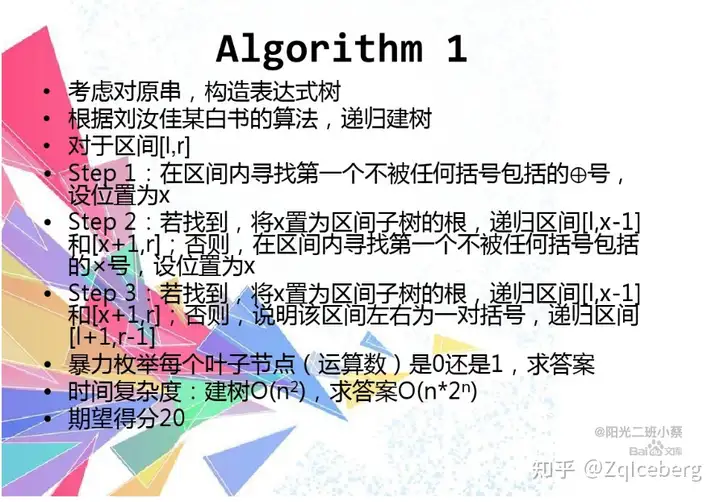
说在后面

• 有好的灵感，不要轻易放过
• 可能当初想到时候，水平有限实现不出来，功力深了后，可以实践灵感

6.关于笛卡尔树的资料

笛卡尔树 - OI Wiki

7.总结

写这道题目的时候，先是发现有几道类似的表达式的题目，一起看了看，发现这个正解，我并不会做，看题解的时候，发现建树的方法繁琐，但我并不会，我就研究一下建树，发现会T，怎么不会T呢，然后又遇见了笛卡尔树和RMQ，我就又学习了一遍，发现虽然还是不会，但是笛卡尔的建树过程，还是很清晰了，（每次我们插入的元素，必然在树的右链的末端。每个结点最多进出右链一次，用一个栈来维护这个过程）

新建一个大小为 n 的空栈。用 top 来标操作前的栈顶，k 来标记当前栈顶。
For i := 1 to n
    k := top
    While 栈非空 且 栈顶元素 > 当前元素 
        k--
    if 栈非空
        栈顶元素.右儿子 := 当前元素
    if k < top
        当前元素.左儿子 := 栈顶元素
    当前元素入栈
    top := k

for (int i = 1; i <= n; i++) {
  int k = top;
  while (k > 0 && h[stk[k]] > h[i]) k--;
  if (k) rs[stk[k]] = i;  // rs代表笛卡尔树每个节点的右儿子
  if (k < top) ls[i] = stk[k + 1];  // ls代表笛卡尔树每个节点的左儿子
  stk[++k] = i;
  top = k;
}