树状数组

前置知识

位运算，二分，倍增，树

目标

树状数组的原理，基本操作

What

基本用途：维护序列的前缀和

令 x = 7， x = 2^2 + 2^1 + 2^0（任意正整数关于 2 的不重复次幂的唯一分解性质）
区间[1, 7] 可以分解成 [1, 4]，[5, 6]，[7, 7] 三个小区间
长度分别是lowbit(4) = 4，lowbit(6) = 2，lowbit(7) = 1

类似上面的拆分，
对于给定的序列 a，我们建立一个数组 c，其中 c[x] 保存序列 a 的区间 [x - lowbit(x) + 1] 中所有数的和

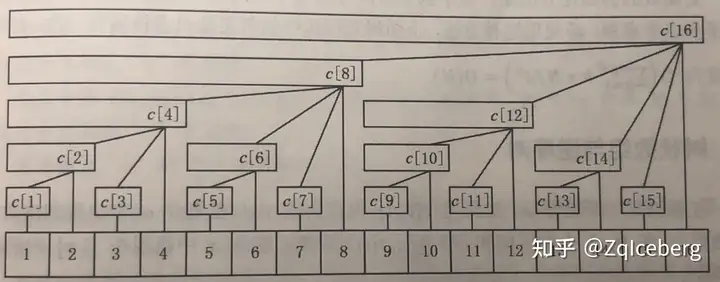
最下边一行是叶子结点，代表数值 a[1 ~ 16]。该结构满足以下性质：
1、每个内部结点 c[x] 保存以它为根的子树中的所有叶子结点的和
2、每个内部结点 c[x] 的子节点个数等于 lowbit(x) 的位数
3、除树根外，每个内部结点 c[x] 的父结点是 c[x + lowbit(x)]
4、树的深度为 O(logn)

如果 n 不是 2 的整次幂，那么树状数组就是一个具有同样性质的森林结构。

基本操作，查询前缀和

int ask(int x) {
    int ans = 0;
    for (; x; x -= x & -x) ans += c[x];
    return ans;
}

区间 [l, r] 的区间和，ask(r) - ask(l - 1)

基本操作，单点增加

给序列中的一个树 a[x] 加上 y，同时正确维护序列的前缀和。

根性树形结构和它的性质，只有结点 c[x] 及其所有祖先结点，保存的区间和，包含 a[x]。
任意一个结点的祖先，至多只有 log(n) 个。
我们逐一对他们的 c 值进行更新即可

void add(int x, int y) {
    for (; x <= n; x += x & -x) c[x] += y;
}

基本操作，初始化

// O(nlogn)
for (int i = 1; i <= n; i++){
    cin >> a[i];
    add(i, a[i]); // 初始化时全部为0，依次修改
}

// 更优雅的初始化, O(n)
// 从小到大依次考虑每个结点 x，借助lowbit运算，扫码它的子节点并求和
// 这样，树形结构中的每条边，只会被遍历一次，时间复杂度为O(n)
int pre[N];
void init(){
    for (int i = 1; i <= n; i++){
        pre[i] = pre[i - 1] + a[i];
        c[i] = pre[i] - pre[i - lowbit(i)];
    }
}

总结

树状数组基于二进制划分与倍增思想

参考

《算法进阶指南》 树状数组 - OI Wiki