拓扑序¶

前置知识¶

建图，BFS

目标¶

拓扑序的模板题

What¶

在计算机科学领域，有向图的拓扑排序或拓扑测序是对其顶点的一种线性排序，使得对于从顶点 u 到顶点 v 的每个有向边 uv，u 在排序中都在 v 之前。

例如，图形的顶点可以表示要执行的任务，并且边可以表示一个任务必须在另一个任务之前执行的约束；在这个应用中，拓扑排序只是一个有效的任务顺序。

当且仅当图中没有定向环时（即有向无环图），才有可能进行拓扑排序。

任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内，构建任何有向无环图的拓扑排序。

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，才能称为该图的一个拓扑排序（英语：Topological sorting）： 1、序列中包含每个顶点，且每个顶点只出现一次； 2、若A在序列中排在B的前面，则在图中不存在从B到A的路径。

Topological sorting拓扑序，看名称有一个sorting的单词，但并不是和快排是一块的东西。

场景：拓扑序，解决具有层级性的问题。 在某校的选课系统中，存在这样的规则：每门课可能有若干门先修课，如果要修读某一门课，则必须要先修读此课程所要求的先修课后才能修读。假设一个学生同时只能修读一门课程，那么，被选课系统允许的他修完他需要所有课程的顺序是一个拓扑序。在这个例子中，每一门课程对应有向图中的一个顶点，每一个先修关系对应一条有向边（从先修课指向需要先修课的课）。

A topological sort is an ordering of the nodes of a directed graph such that if there is a path from node a to node b, then node a appears before node b in the ordering. For example, for the graph one topological sort is [4,1,5,2,3,6]:

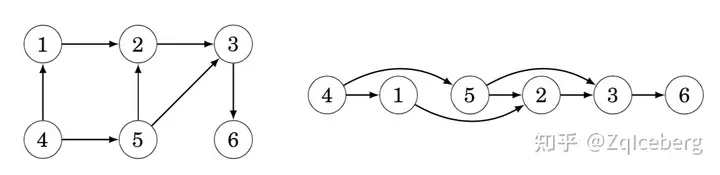
An acyclic(无环的) graph always has a topological sort. However, if the graph contains a cycle, it is not possible to form a topological sort, because no node of the cycle can appear before the other nodes of the cycle in the ordering. It turns out that depth-first search can be used to both check if a directed graph contains a cycle and, if it does not contain a cycle, to construct a topological sort.

topsort就是有向图的宽度优先遍历的应用拓扑序，不唯一如要要字典序最小的拓扑序，在遍历入度为0的点的时候，从1开始遍历，并入队有明显【层级关系】的问题，可以考虑用topsort()模型

How¶

卡恩算法

L ← 包含已排序的元素的列表，目前为空
S ← 入度为零的节点的集合
当 S 非空时：
    将节点n从S移走
    将n加到L尾部
    选出任意起点为n的边e = (n,m)，移除e。如m没有其它入边，则将m加入S。
    重复上一步。
如图中有剩余的边则：
    return error   (图中至少有一个环)
否则： 
    return L   (L为图的拓扑排序)

例题¶

1351：【例4-12】家谱树

#include <bits/stdc++.h>

using namespace std;

const int N = 110, M = 110 * 110;

int h[N], e[M], ne[M], idx;
int n, in[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void topsort()
{
    queue<int> q;
    for (int i = 1; i <= n; i++) if(!in[i]) q.push(i);

    while (!q.empty()){
        int t = q.front(); q.pop();
        printf("%d ", t);

        for (int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            in[j]--;

            if (!in[j]) q.push(j);
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 1; i <= n; i++){
        int x;
        while (cin >> x && x){
            add(i, x);
            in[x]++;
        }
    }

    topsort();
    puts("");

    return 0;
}

题单¶

1352：【例4-13】奖金 1395：烦人的幻灯片(slides) P1347 排序 1964：【13NOIP普及组】车站分级

总结¶

拓扑序，在考纲里是提高组的，但我认为可以在普及组阶段直接学习，练习对图的理解和掌握。