线段树

前置知识

树，二叉树，倍增，ST表

目标

掌握线段树的建立、区间查询、区间修改、延迟标记(lazy-tag)

What

场景：

在序列上，如何快速求出区间和？前缀和

在序列上，如何快速求出最值？ST表

在序列上，偶尔还要修改序列的值，如何快速求助区间和，快速求最值？线段树

线段树(Segment Tree)，是一种特殊的二叉树，可以将一个显性的序列组织成一个树状的结构，从而可以在 \(log\) 的时间复杂度下访问序列上的任意一个区间，并进行维护。需要注意的是，使用线段树维护的信息，必须具有可合并性。

线段树是一种更加通用的数据结构：

1、线段树的每个结点，都代表一个区间

2、线段树具有唯一的根结点，代表的区间是整个统计范围，[1, n]

3、线段树的每个叶子结点，都代表一个长度为1的元区间，[i, i]

4、对于每个内部结点 [l, r]，它的左儿子是 [l, mid], 右儿子是 [mid+1, r]，其中 mid = (l + r) / 2

线段树的存储结构： 1、根结点，编号为 \(1\)

2、编号为 \(x\) 的结点，左儿子是 \(x * 2\)，右儿子是 \(x * 2 + 1\)

可以看出，树的最后一层结点，在数组中保存的位置是不连续的，直接空出数组中多余的位置即可。

在理想情况下，\(n\) 个叶子结点的满二叉树，有 \(n + n / 2 + n / 4 + ... + 2 + 1= 2n - 1\) 个结点。按上述存储方式，父子 \(2\)倍编号方法，最后还有一层产生了空余，所以，保存线段树的数组，长度不应小于\(4n\)，否则可能越界。

线段树基于分治思想

线段树的图例

https://oi-wiki.org/ds/seg/

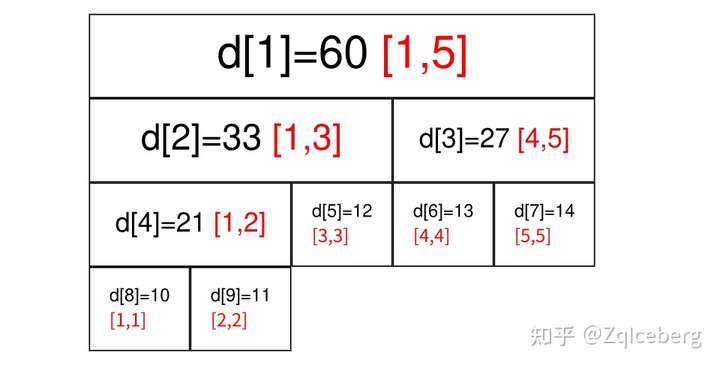
下面这段代码，建立了一个线段树，并在每个结点上保存了对应区间的区间和。

线段树的建树

struct segmentTree {
    int l, r;
    ll dat;
} t[N * 4];

int n, w, a[N];

// build()的时间复杂度是O(n)，因为每调用一次build，就新建了一个线段树结点。（整体分析）
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) {
        t[p].dat = a[l];
        return ;
    }

    int mid = (l + r) / 2;
    build(p * 2, l, mid);
    build(p * 2 + 1, mid + 1, r);

    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
}

线段树的单点修改

void change(int p, int x, int y) {
    if (t[p].l == t[p].r) {
        t[p].dat += y;
        return ;
    }

    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p * 2, x, y);
    else change(p * 2 + 1, x, y);

    // 回溯的时候，由子区间的区间和，更新当前区间的和
    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat; 
}

线段树的区间查询

区间查询的流程：

从根开始递归，如果当前结点所代表的区间 [L, R] 被所查询的区间 [l, r] 所包含，那么直接返回当前区间的和。

如果两个区间没有交集，返回 0。

如果没有被包含，并且两区间有交集，递归左右子结点。

ll ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含

    ll sum = 0;
    int mid = (t[p].l + t[p].r) / 2;
    if (l <= mid) sum += ask(p * 2, l, r);    // 左子结点有重叠
    if (r > mid) sum += ask(p * 2 + 1, l, r); // 右子结点有重叠

    return sum;
}

例题，单点修改，区间查询，P2068 统计和- 洛谷

题意，每次询问两种操作，x a b，表示在第 a 个数上加上 b。y a b，表示输出 a 到 b 区间和。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

struct segmentTree {
    int l, r;
    ll dat;
} t[N * 4];

int n, w, a[N];

// 查询的区间 [l, r]
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) {
        t[p].dat = a[l];
        return ;
    }

    int mid = (l + r) / 2;
    build(p * 2, l, mid);
    build(p * 2 + 1, mid + 1, r);

    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
}

void change(int p, int x, int y) {
    if (t[p].l == t[p].r) {
        t[p].dat += y;
        return ;
    }

    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p * 2, x, y);
    else change(p * 2 + 1, x, y);

    t[p].dat = t[p * 2].dat + t[p * 2 + 1].dat;
}

// 查询的区间 [l, r]
ll ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含

    ll sum = 0;
    int mid = (t[p].l + t[p].r) / 2;
    if (l <= mid) sum += ask(p * 2, l, r);    // 左子结点有重叠
    if (r > mid) sum += ask(p * 2 + 1, l, r); // 右子结点有重叠

    return sum;
} 

int main() {
    cin >> n >> w;

    build(1, 1, n);

    while (w--) {
        char op[2];
        int x, y;
        scanf("%s%d%d", op, &x, &y);

        if (op[0] == 'x') change(1, x, y);
        else cout << ask(1, x, y) << '\n';
    }

    return 0;
}

例题，单点修改，区间查询，维护多种多样的信息，最大子段和，GSS3 - Can you answer these queries III

题意：q 次操作，0 x y，表示把第 x 个数修改成 y。1 l r，表示询问区间 [l, r] 的最大子段和 在线段树上的每个结点，除了区间端点外，再维护 \(4\) 个信息：

区间和 sum，

区间最大连续子段和 dat，

紧靠左端的最大连续子段和 lmax，

紧靠右端的最大连续子段和 rmax。

线段树的整体框架不变，在 build 和 change 函数中，更新回溯的部分。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

struct SegmentTree {
    int l, r;
    ll sum, dat, lmax, rmax;
} t[N * 4];

int n, q, a[N];

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) {
        t[p].sum = t[p].dat = t[p].lmax = t[p].rmax = a[l];
        return ;
    }

    int mid = (l + r) / 2;
    build(p * 2, l, mid);
    build(p * 2 + 1, mid + 1, r);

    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;
    t[p].lmax = max(t[p * 2].lmax, t[p * 2].sum + t[p * 2 + 1].lmax);
    t[p].rmax = max(t[p * 2 + 1].rmax, t[p* 2 + 1].sum + t[p * 2].rmax);
    t[p].dat = max(max(t[p * 2].dat, t[p * 2 + 1].dat), t[p * 2].rmax + t[p * 2 + 1].lmax);
}

void change(int p, int x, int y) {
    if (t[p].l == t[p].r) {
        t[p].sum = t[p].dat = t[p].lmax = t[p].rmax = y;
        return ;
    }

    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p * 2, x, y);
    else change(p * 2 + 1, x, y);

    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;
    t[p].lmax = max(t[p * 2].lmax, t[p * 2].sum + t[p * 2 + 1].lmax);
    t[p].rmax = max(t[p * 2 + 1].rmax, t[p* 2 + 1].sum + t[p * 2].rmax);
    t[p].dat = max(max(t[p * 2].dat, t[p * 2 + 1].dat), t[p * 2].rmax + t[p * 2 + 1].lmax);
}

SegmentTree ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p]; // 完全包含

    SegmentTree a, b, ans;
    a.sum = a.lmax = a.rmax = a.dat = -1e18;
    b.sum = b.lmax = b.rmax = b.dat = -1e18;
    ans.sum = 0;

    int mid = (t[p].l + t[p].r) / 2;
    if (l <= mid) { // 左子结点有重叠
        a = ask(p * 2, l, r);
        ans.sum += a.sum;
    }
    if (r > mid) { // 右子结点有重叠
        b = ask(p * 2 + 1, l, r);
        ans.sum += b.sum;
    }

    ans.dat = max(max(a.dat, b.dat), a.rmax + b.lmax);
    ans.lmax = max(a.lmax, a.sum + b.lmax);
    ans.rmax = max(b.rmax, b.sum + a.rmax);

    // 讨论一下特殊情况
    if (l > mid) ans.lmax = max(ans.lmax, b.lmax);
    if (r <= mid) ans.rmax = max(ans.rmax, a.rmax);

    return ans;
} 

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

    build(1, 1, n);

    cin >> q;
    while (q--) {
        int op, x, y;
        scanf("%d%d%d", &op, &x, &y);

        if (op == 0) change(1, x, y);
        else cout << ask(1, x, y).dat << '\n';
    }

    return 0;
}

AC代码

从这道题目，我们可以看出，线段树作为一种比较通用的数据结构，能够维护各式各样的信息，前提是这些信息容易按照区间进行划分与合并（又称满足区间可加性）。

我们只需要在父子传递信息和更新答案时，稍作变化即可。

区间修改，区间查询

在区间修改时，显然不能暴力地修改每个叶子结点，效率很低。

引入延迟标记（lazy-tag），记录一些区间修改的信息。

当递归到一个被完全包含的区间时，在这个区间打上一个延迟标记，记录这个区间中的每个数都需要被加上某个数，然后，直接修改该结点的区间和并返回，不再向下递归。

当新访问到一个结点时，先将延迟标记下放到子结点，然后再进行递归。

对于打了延迟标记的结点，维护的区间和是已经完成修改的值，其子结点的值，还没有被修改。 也就是说，延迟标记起到的作用是记录子结点的每个数应该加上多少，而不是该结点本身的信息。

在标记下传后，应该清空当前结点的延迟标记，并且必须先判断区间在当前内，再进行 \(pushdown\)，否则一旦在叶子结点 \(pushdown\)，可能会造成数组越界。

int lzy[N * 4];

void pushup(int u) {
    w[u] = w[u * 2] + w[u * 2 + 1];
}

void maketag(int u, int len, int x){
    lzy[u] += x;
    w[u] += len * x;  // 修改当前结点的区间和
}

// 当前结点u所代表的区间 [L, R]
void pushdown(int u, int L, int R){
    int mid = (L + R) >> 1;
    maketag(u * 2, mid - L + 1, lzy[u]);  // 左子树加上lzy[u]
    maketag(u * 2 + 1, R - mid, lzy[u]);    // 右子树加上lzy[u]
    lzy[u] = 0;  // lzy[u]已经下放，清空
}

// 当前结点u所代表的区间 [L, R]
// 查询的区间 [l, r]
int query(int u, int L, int R, int l, int r){
    if (InRange(L, R, l, r)) return w[u]; // [l,r]完全包含[L,R]，直接返回区间和
    else if (!OutofRange(L, R, l, r)){ // 有交集
        int mid = (L + R) >> 1;

        pushdown(u, L, R); // 查询的时候，需要将结点标记下放
        return query(u * 2, L, mid, l, r) + query(u * 2 + 1, mid + 1, R, l, r);
    }
    else return 0;
}

// 当前结点u所代表的区间 [L, R]
// 查询的区间 [l, r]
void upd(int u, int L, int R, int l, int r, int x){
    if (InRange(L, R, l, r)) maketag(u, R - L + 1, x);   // 完全包含，直接打标记
    else if (!OutofRange(L, R, l, r)){
        int mid = (L + R) >> 1;

        pushdown(u, L, R); // 注意，必须先将当前结点的标记下传，才能递归修改下面的结点
        upd(u * 2, L, mid, l, r, x);
        upd(u * 2 + 1, mid + 1, R, l, r, x);

        pushup(u); // 维护区间和
    }
}

例题，区间修改，区间查询，P3372 【模板】线段树 1

题意：对一个数列，进行两种操作

1、将某区间上的每一个数加上 k

2、求某区间和

思路：线段树的每个结点上保存了 sum（区间和），add（增量延迟标记）。

建树、查询和修改的框架保持不变，spread 函数实现了延迟标记的向下传递。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

struct segmentTree {
    int l, r;
    ll sum, add;
} t[N * 4];

int n, m, a[N];

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) {
        t[p].sum = a[l];
        t[p].add = 0;
        return ;
    }

    int mid = (l + r) / 2;
    build(p * 2, l, mid);
    build(p * 2 + 1, mid + 1, r);

    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;
}

void spread(int p) {
    // 首先判断结点 p 是否有标记
    if (t[p].add != 0) {                
        t[p * 2].sum += t[p].add * (t[p * 2].r - t[p * 2].l + 1); // 更新左儿子
        t[p * 2 + 1].sum += t[p].add * (t[p * 2 + 1].r - t[p * 2 + 1].l + 1); // 更新右儿子

        t[p * 2].add += t[p].add; // 给左儿子打上延迟标记
        t[p * 2 + 1].add += t[p].add; // 给右儿子打上延迟标记

        t[p].add = 0; // 清除自己的延迟标记
    }
}


void change(int p, int x, int y, int k) {
    // 结点p代表的区间，被[x, y]完全包含
    if (x <= t[p].l && y >= t[p].r) {
        t[p].sum += 1ll * k * (t[p].r - t[p].l + 1);
        t[p].add += k;
        return ;
    }

    spread(p);

    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p * 2, x, y, k);
    if (y > mid) change(p * 2 + 1, x, y, k);

    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;
}

ll ask(int p, int l, int r) {
    // 结点p代表的区间，被[l, r]完全包含
    if (l <= t[p].l && r >= t[p].r) return t[p].sum; 

    spread(p);

    ll sum = 0;
    int mid = (t[p].l + t[p].r) / 2;
    if (l <= mid) sum += ask(p * 2, l, r);    // 左子结点有重叠
    if (r > mid) sum += ask(p * 2 + 1, l, r); // 右子结点有重叠

    return sum;
} 

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

    build(1, 1, n);

    while (m--) {
        int op;
        int x, y, k;
        scanf("%d", &op);

        if (op == 1) {
            scanf("%d%d%d", &x, &y, &k);
            change(1, x, y, k);
        }
        else {
            scanf("%d%d", &x, &y);
            printf("%lld\n", ask(1, x, y));
        }
    }

    return 0;
}

以下是同学的其他版本代码，在教程的历史版本中存在，保留下来以纪念。

@赵蝙蝠的版本

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
struct node{
    long long l, r, lazy = 0, w, len;
} tree[N * 4];
long long mp[N];
void build(int p, int l, int r){
    tree[p].l = l, tree[p].r = r, tree[p].len = r - l + 1;
    if (l == r)
        tree[p].w = mp[l];
    else{
        int mid = (l + r) >> 1;
        build(p << 1, l, mid), build(p << 1 | 1, mid + 1, r);
        tree[p].w = tree[p << 1].w + tree[p << 1 | 1].w;
    }
}
void pushdown(int p){
    int k = tree[p].lazy;
    tree[p].lazy = 0;
    tree[p << 1].lazy += k, tree[p << 1].w += tree[p << 1].len * k;
    tree[p << 1 | 1].lazy += k, tree[p << 1 | 1].w += tree[p << 1 | 1].len * k;
}
void pushup(int p) { tree[p].w = tree[p << 1].w + tree[(p << 1) + 1].w; }
void update(int p, int l, int r, long long k){
    if (tree[p].l >= l && tree[p].r <= r)
        tree[p].lazy += k, tree[p].w += tree[p].len * k;
    else if (tree[p].l > r || tree[p].r < l) return;
    else{
        pushdown(p);
        update(p << 1, l, r, k), update(p << 1 | 1, l, r, k);
        pushup(p);
    }
}
long long get(int p, int l, int r){
    if (tree[p].l >= l && tree[p].r <= r) return tree[p].w;
    if (tree[p].l > r || tree[p].r < l) return 0;
    pushdown(p);
    return get(p << 1, l, r) + get(p << 1 | 1, l, r);
}
int main(){
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%lld", &mp[i]);
    build(1, 1, n);
    while (m--){
        long long op, x, y, k;
        scanf("%lld %lld %lld", &op, &x ,&y);
        if (op == 2)
            printf("%lld\n",get(1, x, y));
        else{
            scanf("%lld", &k);
            update(1, x, y, k);
        }
    }
    return 0;
}

@赵蝙蝠，指针版本

#include <bits/stdc++.h>
using namespace std;
typedef long long lol;
#define fr(i, s, e)  for (auto i = s; i <= e; i++)
#define iff(i, s, e) (i) ? (s) : (e)
#define pb(a)        emplace_back(a)
#define ckr \
    if (root == nullptr) return;
lol mp[100010];
struct node {
    node *l = nullptr, *r = nullptr;
    lol w = 0, lz = 0, ll, rr, len;
};
void maketag(node *root, int k) { ckr root->w += root->len * k, root->lz += k; }
void pushdown(node *root) {
    ckr maketag(root->l, root->lz), maketag(root->r, root->lz);
    root->lz = 0;
}
lol get(node *root) { return (root == nullptr) ? (0) : (root->w); }
void pushup(node *root) { ckr root->w = get(root->l) + get(root->r); }
void update(node *root, int l, int r, int k) {
    if (root == nullptr || root->rr < l || root->ll > r)
        return;
    else if (root->ll >= l && root->rr <= r)
        maketag(root, k);
    else {
        pushdown(root);
        update(root->l, l, r, k), update(root->r, l, r, k);
        pushup(root);
    }
}
lol sum(node *root, int l, int r) {
    if (root == nullptr || root->rr < l || root->ll > r)
        return 0;
    else if (root->ll >= l && root->rr <= r)
        return root->w;
    else {
        pushdown(root);
        return sum(root->l, l, r) + sum(root->r, l, r);
    }
}
void build(node *root, int l, int r) {
    root->ll = l, root->rr = r, root->len = r - l + 1;
    if (l == r)
        root->w = mp[l];
    else {
        int mid = (l + r) >> 1;
        node *ls = new (node), node *rs = new (node);
        build(ls, l, mid), build(rs, mid + 1, r);
        root->l = ls, root->r = rs;
        pushup(root);
    }
}
int main() {
    node *root = new (node);
    int n, m;
    cin >> n >> m;
    fr(i, 1, n) cin >> mp[i];
    build(root, 1, n);
    fr(i, 1, m) {
        int op, l, r, k;
        cin >> op >> l >> r;
        if (op == 1) {
            cin >> k;
            update(root, l, r, k);
        } else
            cout << sum(root, l, r) << endl;
    }
    return 0;
}

总结

关于延迟标记，试想，我们在一次修改中，发现结点 \(p\) 代表的区间，被修改区间 \([l, r]\) 完全覆盖，并且逐一更新了子树 \(p\) 中的所有结点，但是在之后的查询中，却根本没有用到 \([l, r]\) 的子区间作为候选答案，那么更新 \(p\) 的整颗子树就是徒劳的。

换句话说，我们在进行区间修改时，如果发现结点 \(p\) 代表的区间，被 $[l, r] $ 完全覆盖，就应该立即返回，只不过在回溯之前，向结点 \(p\) 增加一个标记，标记“该结点曾经被修改，但其子结点尚未被更新”。

如果在后续的指令中，需要从结点 \(p\) 向下递归，我们再检查 \(p\) 是否具有标记。如果有标记，就根据标记信息更新 \(p\) 的两个儿子结点，同时，为 \(p\) 的两个儿子结点增加标记，然后清除 \(p\) 的标记。

延迟标记，提供了线段树中从上往下传递信息的方式。

“延迟”思想，是设计算法与解决问题的一个重要思路。

题单

【模板】线段树 1 - 洛谷

[TJOI2009] 开关 - 洛谷

无聊的数列 - 洛谷

扶苏的问题 - 洛谷

【模板】线段树 2 - 洛谷

小白逛公园 - 洛谷

参考

https://oi-wiki.org/ds/seg/

《算法竞赛进阶指南》

《深入浅出程序设计竞赛》