差分约束

前置知识

最短路

目标

差分约束的定义，模板题

What

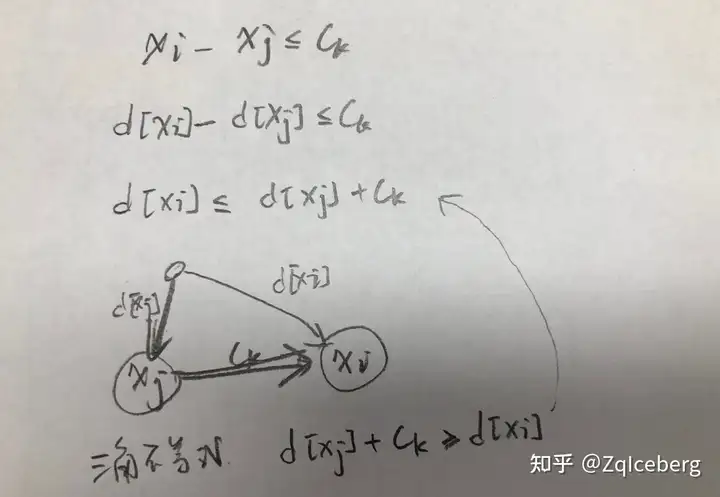
把Xi看作有向图中的一个结点i，对于每个约束条件 xj - xi <= ck，理解成结点 j 指向结点 i 连一条长度为 ck的有向边。计算单源最短路，若图中存在负环，则给定的差分约束系统无解。 对于一些题目中，约束条件形如xi - xj >= ck。（前面是<=ck，不一样）我们仍然可以从 j 到 i 连长度为 ck 的有向边，只是改为计算单源最长路，若图中有正环则无解。

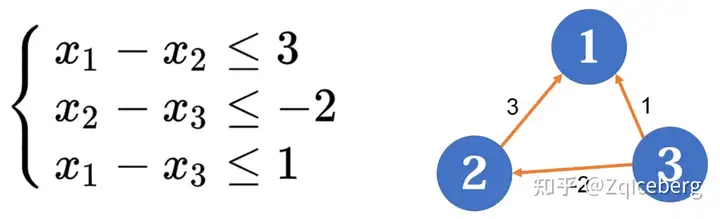
例题

Intervals - Virtual Judge

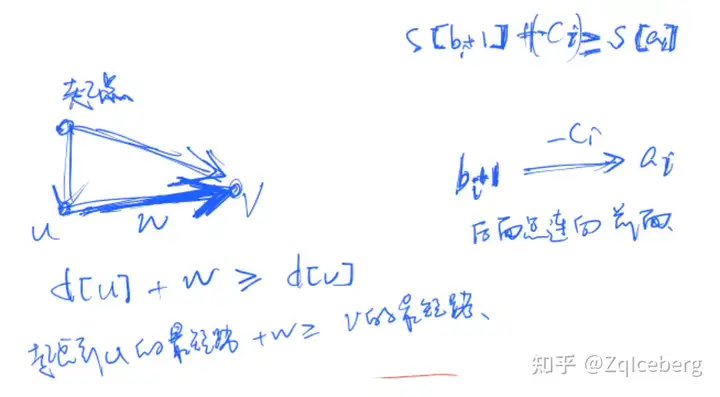
题意：n个区间，每个区间[ai, bi]，至少有ci的元素被选。这个集合里面，最少需要有多少个元素 思路：s[k]表示[0, k]之间最少选出多少个整数。s[bi] - s[ai-1]>= ci，明显是一个差分约束系统。 s[ai - 1]存在下标不好处理的情况，下标从1开始，处理成 s[bi + 1] - s[ai] >= ci，这样就好处理了。 ai 向 bi+1 ,连一条边，边长是ci，求最长路。

// 代码01
// 思路，最长路，从前往后找，就是最长路
// 最长路的定义与最短路是对偶的
#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

const int N = 1e6, INF = 2e9;

int h[N], e[N], ne[N], w[N], idx;
bool st[N];
int maxn, minn;
int dist[N];
int n;

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void spfa()
{
    for (int i = minn; i <= maxn; i++) dist[i] = -INF;

    queue<int> q;
    q.push(minn);
    dist[minn] = 0;

    while (!q.empty())
    {
        int t = q.front(); q.pop();
        st[t] = false;  //标记在不在队列里

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[t] + w[i] > dist[j])
            {
                dist[j] = dist[t] + w[i];

                if (!st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
}

int main()
{
    scanf("%d", &n);

    memset(h, -1, sizeof h);
    maxn = -INF, minn = INF;

    for (int i = 1; i <= n; i++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        // s[b] - s[a-1] >= c
        // s[b+1] - s[a] >= c  平移一个下标
        minn = min(minn, a);
        maxn = max(maxn, b + 1);

        add(a, b + 1, c);
                // s[b+1] - s[a] >= c, s[i]表示前i个位置有几个数
                // a向b+1连了一条线，求最长路
    }

        // s[i+1] - s[i] >= 0，表示[1,i+1]之间选出的 数，肯定比[1, i]要多
        // s[i+1] - s[i] <= 1，表示每个数只能被选一次。可变形为s[i] - s[i + 1] >= -1，变成求最长路的模型
    for (int i = minn; i < maxn; i++)
    {
        add(i, i + 1, 0);
        add(i + 1, i, -1);
    }

    spfa();

    printf("%d\n", dist[maxn]);

    return 0;
}

// 代码02，最短路
// 从后往前找，就是最短路。注意，边长是相反数，输出的时候，反过来
#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

const int N = 1e6, INF = 2e9;

int h[N], e[N], ne[N], w[N], idx;
bool st[N];
int maxn, minn;
int dist[N];
int n;

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void spfa()
{
    for (int i = minn; i <= maxn; i++) dist[i] = INF;

    queue<int> q;
    q.push(maxn);
    dist[maxn] = 0;

    while (!q.empty())
    {
        int t = q.front(); q.pop();
        st[t] = false;  //标记在不在队列里

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[t] + w[i] < dist[j])
            {
                dist[j] = dist[t] + w[i];

                if (!st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
}

int main()
{
    scanf("%d", &n);

    memset(h, -1, sizeof h);
    maxn = -INF, minn = INF;

    for (int i = 1; i <= n; i++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        //s[b] - s[a-1] >= c
        //s[b+1] - s[a] >= c  平移一个下标
        minn = min(minn, a);
        maxn = max(maxn, b + 1);

        c = -c;
        add(b + 1, a, c);
    }

    //超级原点
    for (int i = minn; i < maxn; i++)
    {
        add(i + 1, i, 0);
        add(i, i + 1, 1);
    }

    spfa();

    printf("%d\n", -dist[minn]);

    return 0;
}

题单

Intervals - Virtual Judge 【模板】差分约束算法 - 洛谷 种树 - 洛谷 THE MATRIX PROBLEM - Virtual Judge King Berl VI - Virtual Judge [HNOI2005]狡猾的商人 - 洛谷 [SCOI2011]糖果 - 洛谷

总结

对于差分不等式，a - b <= c ，建一条 b 到 a 的权值为 c 的边，求的是最短路 对于不等式 a - b >= c ，建一条 b 到 a 的权值为 c 的边，求的是最长路 设x[i]是第i位置（或时刻）的值（跟所求值的属性一样），那么把x[i]看成数列，前n项和为s[n]，则x[i] = s[i] - s[i-1]。那么这样就可以最起码建立起类似这样的一个关系：0 <= s[i] - s[i-1] <= 1 难点在于建图 最长路的定义与最短路是对偶的

参考

差分约束 - OI Wiki 7.7 图基础算法之差分约束系统_哔哩哔哩_bilibili Pecco：算法学习笔记(11): 差分约束 作业部落 Cmd Markdown 编辑阅读器