笛卡尔树

前置知识

平衡树，堆

目标

模板题

What

笛卡尔树是一种特定的二叉树数据结构，可由数列构造，在范围最值查询、范围 top k 查询等问题有广泛应用。它具有堆的有序性，中序遍历可以输出原数列。从数列中构造一棵笛卡尔树可以线性时间完成，采用基于栈的算法来找到在该数列中的所有最近小数。

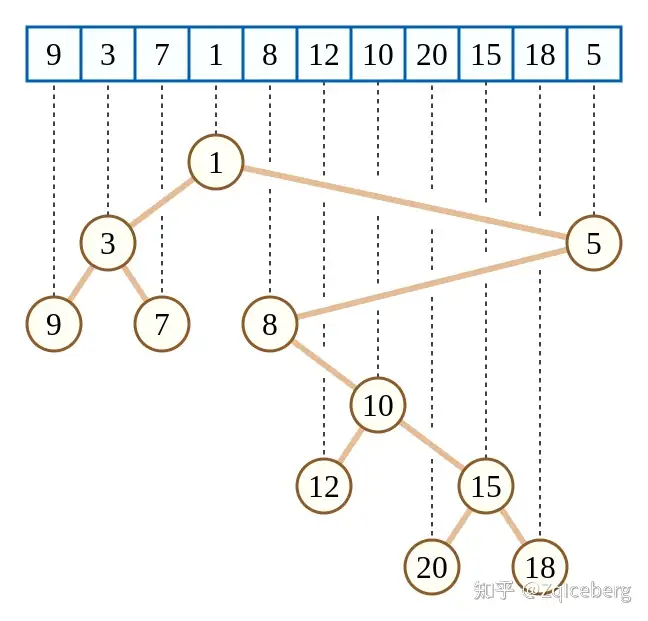
笛卡尔树的构建

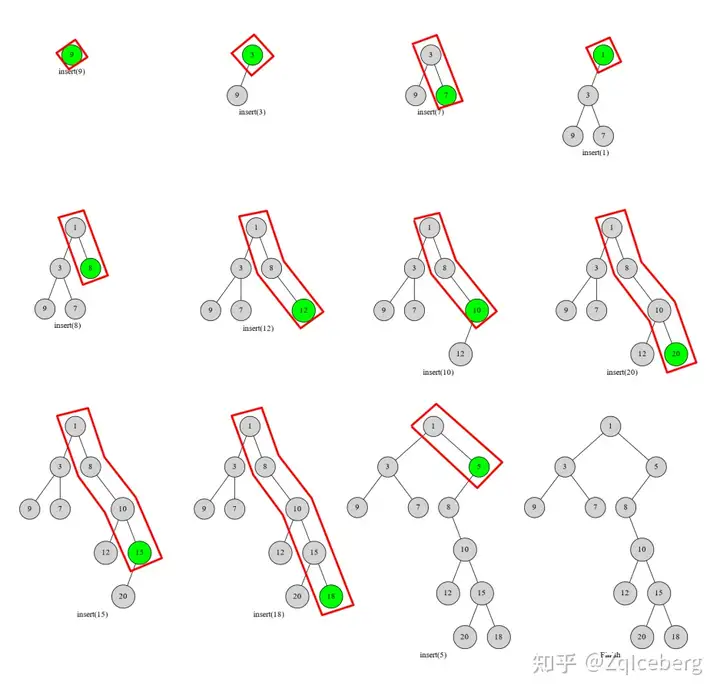
新建一个大小为 n 的空栈。用 top 来标操作前的栈顶，k 来标记当前栈顶。

For i := 1 to n
    k := top
    While 栈非空 且 栈顶元素 > 当前元素 
        k--
    if 栈非空
        栈顶元素.右儿子 := 当前元素
    if k < top
        当前元素.左儿子 := 栈顶元素
    当前元素入栈
    top := k

例题，2201 -- Cartesian Tree

// 关键点
// int id[N], key[N], value[N];
// int ch[N][2], parent[N], stk[N];
// int tt;

#include <bits/stdc++.h>

using namespace std;

const int N = 50010;

int id[N], key[N], value[N];
int ch[N][2], parent[N], stk[N];
int tt;
int n;

bool cmp(int i, int j){
    return key[i] < key[j];
}

int main(){
    cin >> n;
    for (int i = 1; i <= n; i++){
        cin >> key[i] >> value[i];
        id[i] = i;
    }

    sort(id + 1, id + 1 + n, cmp);

    for (int s = 1; s <= n; s++){
        int i = id[s];
        int j, p = 0;  // p表示刚刚退出栈的, 题意无儿子用0代替
        while (tt > 0 && value[stk[tt]] > value[i]){
            j = stk[tt--];      // 刚刚退出栈的是谁
            ch[j][1] = p;       // 刚刚退栈的右儿子赋值成上一个退掉的p
            parent[p] = j;      // 上一个退栈的父亲是j
            p = j;              // p更新，进行下一轮
        }

        ch[i][0] = p;   // 左儿子等于上一个退栈的p
        parent[p] = i;
        stk[++tt] = i;  // i加入栈里
    }

    // 最后清空一下栈的里东西
    int j, p = 0;
    while (tt > 0){
        j = stk[tt--];
        ch[j][1] = p;
        parent[p] = j;
        p = j;
    }

    // 笛卡尔树的构造方式，决定了肯定有解
    cout << "YES" << '\n';
    for (int i = 1; i <= n; i++)
        cout << parent[i] << ' ' << ch[i][0] << ' ' << ch[i][1] << '\n';

    return 0;
}

题单

2201 -- Cartesian Tree 【模板】笛卡尔树 - 洛谷 https://vjudge.net/problem/HDU-1506 [TJOI2011] 树的序 - 洛谷 [AGC028B] Removing Blocks [AGC024E] Sequence Growing Hard

总结

笛卡尔树是二叉树，对于数列而言将其作为二叉搜索树是自然的。若将二叉搜索树结点关联上一个权值，并且保证此权值在树结构中遵循堆中的序关系，及父结点权值比子结点权值大，则此二叉搜索树又被称为Treap（tree + heap -> treap）。Treap 与笛卡尔树在结构上是相同的，只是两者的应用不同。

参考

笛卡尔树 - OI Wiki