分块¶
前置知识¶
树状数组，线段树
目标¶
分块思想，模板题
What¶
树状数组基于二进制划分与倍增思想，线段树基于分治思想。 二者把序列中的元素聚合成大大小小的“段”，花费额外的代价，对“段”进行维护，从而使得每个区间的信息可以快速由几个已有的“段”结合而成。 分块的基本思想是，通过适当的划分，预处理一部分信息并保存下来，用空间换取时间，达到时空平衡。
例题，POJ3468 A Simple Problem with Integers¶
题意，对一个数组进行两种操作，“C a b c”，对[a, b]区间加上c，“Q a b" 查询[a, b]区间的和
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll arr[N], sum[N], add[N];
int L[N], R[N]; // each segment [l, r]
int bel[N]; // maintain the point belong which segment
int n, T, B;
void change(int l, int r, int d) {
int p = bel[l], q = bel[r];
// belong to a same block
if (p == q) {
for (int i = l; i <= r; i++) arr[i] += d;
sum[p] += 1ll * (r - l + 1) * d;
}
else {
for (int i = p + 1; i <= q - 1; i++) add[i] += d;
for (int i = l; i <= R[p]; i++) arr[i] += d;
sum[p] += 1ll * (R[p] - l + 1) * d;
for (int i = L[q]; i <= r; i++) arr[i] += d;
sum[q] += 1ll * (r - L[q] + 1) * d;
}
return ;
}
ll ask(int l, int r) {
int p = bel[l], q = bel[r];
ll ret = 0;
if (p == q) {
for (int i = l; i <= r; i++) ret += arr[i];
ret += add[p] * (r - l + 1);
}
else {
for (int i = p + 1; i <= q - 1; i++) ret += sum[i] + add[i] * (R[i] - L[i] + 1);
for (int i = l; i <= R[p]; i++) ret += arr[i];
ret += add[p] * (R[p] - l + 1);
for (int i = L[q]; i <= r; i++) ret += arr[i];
ret += add[q] * (r - L[q] + 1);
}
return ret;
}
int main() {
cin >> n >> T;
for (int i = 1; i <= n; i++) scanf("%lld", &arr[i]);
// sqrt
B = sqrt(1.0 * n);
for (int i = 1; i <= B; i++) {
L[i] = (i - 1) * B + 1;
R[i] = i * B;
}
if (R[B] < n) {
B++;
L[B] = R[B - 1] + 1;
R[B] = n;
}
// init
for (int i = 1; i <= B; i++)
for (int j = L[i]; j <= R[i]; j++) {
bel[j] = i;
sum[i] += arr[j];
}
// ask and answer
while (T--) {
char op[3];
int l, r, d;
scanf("%s%d%d", op, &l, &r);
if (op[0] == 'C') {
scanf("%d", &d);
change(l, r, d);
}
else printf("%lld\n", ask(l ,r));
}
return 0;
}
段数 和 段长，都是 � ，所以，整个算法的时间复杂度为 �((�+�)∗�) 。
题单¶
POJ3468 A Simple Problem with Integers LOJ#6280. 数列分块入门 4 UVA-12003Array Transformer Codeforces - Destiny Codeforces - Holes Codeforces - XOR and Favorite Number Codeforces - Powerful array
总结¶
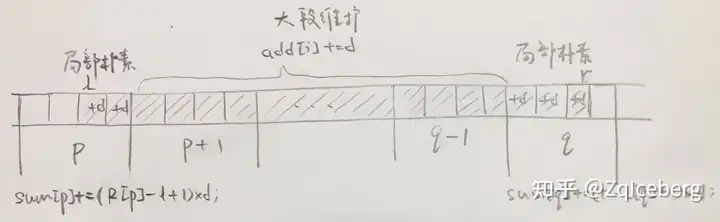
常见的分块思想，可以用“大段维护、局部朴素”来形容。