Treap

前置知识

二叉搜索树

目标

Treap基本操作，代码模板

What

A treap is a binary tree that maintains simultaneously the property of binary search tree (BST) and heap. A treap (tree + heap) is a binary tree whose nodes contain two values, a key and a priority , such that the key keeps the BST property and the priority is a random value that keeps the heap property (it doesn’t matter if it’s a max-heap or min-heap). A treap use the principle of binary trees formed from a random permutation in order to maintain a balanced binary search tree dynamically as nodes are inserted and deleted.

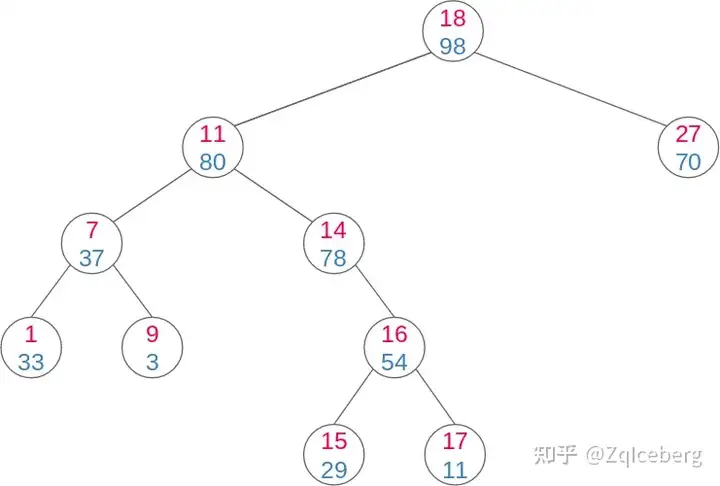
我们在维持 BST 性质的基础上，通过改变二叉搜索树的形态，使得树上每个结点的左右子树大小达到平衡，从而使整棵树的深度维持在O(logn)级别。 改变形态并保持 BST 性质的方法，叫做“旋转”。左旋转（Left Rotation）和右旋转（Right Rotation）。

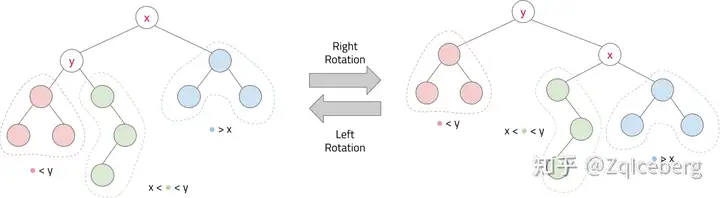
在初始情况下，y 是 x 的左子结点，绿子树是 y 的右子树。 “右旋”操作，x 变为 y 的右子结点， y 原来的右子树（绿子树），变为 x 的左子树。

在初始情况下，x 是 y 的右子结点，绿子树是 x 的左子树。 “左旋”操作，y 变为 x 的左子结点，x 原来的左子树（绿子树），变为 y 的右子树。

// Right Rotate
void right_rotation(int &p) {
    int q = a[p].l;
    a[p].l = a[q].r, a[q].r = p;
    p = q;
}

// Left Rotate
void left_rotation(int &p) {
    int q = a[p].r;
    a[p].r = a[q].l, a[q].l = p;
    p = q;
}

Treap 的思想，就是利用“随机”，来创造平衡条件。在旋转过程中必须维持 BST 性质，所以 Treap 就把“随机”作用在堆的性质上。Treap 在插入一个新结点时，给该结点随机生成一个额外的权值。然后像二叉堆的插入过程一样，自底向上依次检查，当某个结点不满足大根堆性质时，就执行旋转操作，使该结点与其父结点的关系发生交换。

例题，【模板】普通平衡树 - 洛谷

题意：插入x，删除x，查询x的排名，查询排名x的是什么，求x的前驱，求x的后继 数据中可能有相同的数值，我们给每个结点增加一个域 cnt，记录该结点的“副本数”，初始为1。若插入已经存在的数值，就直接把“副本数”加1。在删除时，减少结点的“副本数”，当减为0时，删除该结点。这样就可以容易的处理关键码相同的问题。 题意还要查询排名，我们给每个结点增加一个域 size，记录以该结点为根的子树，所有结点的“副本数”之和。 与线段树一样，我们在插入和删除时，从下往上更新 size 信息。发生旋转操作时，也要更新 size。最后，在 BST 的基础上，通过判断左、右子树 size 的大小，选择适当的一侧递归，就可以查询排名了。Treap的形态会发生变化，我们用递归实现更新，以便于在回溯时，更新 Treap 上存储的 size 信息。

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

struct node {
    int l, r;
    int val, dat; // 结点的关键码和权值
    int cnt, sz; // 副本数，子树大小
}a[N];

int tot, root, n, INF = 0x3f3f3f3f;

int New(int val) {
    a[++tot].val = val;
    a[tot].dat = rand();
    a[tot].cnt = a[tot].sz = 1;
    return tot;
}

void upd(int p) { // 更新子树大小
    a[p].sz = a[a[p].l].sz + a[a[p].r].sz + a[p].cnt;
}

void build() {
    New(-INF), New(INF);
    root = 1, a[1].r = 2; // 无穷小，无穷大
    upd(root);
}

void rightRotate(int &p) {
    int q = a[p].l;
    a[p].l = a[q].r, a[q].r = p, p = q;
    upd(a[p].r), upd(p);
}

void leftRotate(int &p) {
    int q = a[p].r;
    a[p].r = a[q].l, a[q].l = p, p = q;
    upd(a[p].l), upd(p);
}

void insert(int &p, int val) {
    if (p == 0) {
        p = New(val);
        return ;
    }

    if (val == a[p].val) {
        a[p].cnt++, upd(p);
        return ;
    }

    if (val < a[p].val) {
        insert(a[p].l, val);
        if (a[p].dat < a[a[p].l].dat) rightRotate(p); // 右旋
    }
    else {
        insert(a[p].r, val);
        if (a[p].dat < a[a[p].r].dat) leftRotate(p); // 左旋
    }
    upd(p);
}

void remove(int &p, int val) {
    if (p == 0) return ;
    if (val == a[p].val) {
        if (a[p].cnt > 1) {
            a[p].cnt--, upd(p);
            return ;
        }   

        if (a[p].l || a[p].r) { // 不是叶子结点，并且只有一个副本，删掉就要旋转操作
            if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat) {
                rightRotate(p), remove(a[p].r, val);
            }
            else {
                leftRotate(p), remove(a[p].l, val);
            }

            upd(p);
        }
        else p = 0; // 叶子节点，直接删除

        return ;
    }

    if (val < a[p].val) remove(a[p].l, val);
    else remove(a[p].r, val);

    upd(p);
}

int getRankByVal(int p, int val) {
    if (p == 0) return 0;
    if (val == a[p].val) return a[a[p].l].sz + 1;

    if (val < a[p].val) return getRankByVal(a[p].l, val);
    return getRankByVal(a[p].r, val) + a[a[p].l].sz + a[p].cnt; // 在右子树里
}

int getValByRank(int p, int Rank) {
    if (p == 0) return INF;
    if (a[a[p].l].sz >= Rank) return getValByRank(a[p].l, Rank); // 在左子树里
    if (a[a[p].l].sz + a[p].cnt >= Rank) return a[p].val; 
    return getValByRank(a[p].r, Rank - a[a[p].l].sz - a[p].cnt);
}

int getPre(int val) {
    int ans = 1; // 无穷小
    int p = root;
    while (p) {
        if (val == a[p].val) {
            if (a[p].l > 0) {
                p = a[p].l;
                while (a[p].r > 0) p = a[p].r; // 左子树上一直向右走
                ans = p;
            }
            break;
        }

        if (a[p].val < val && a[p].val > a[ans].val) ans = p;
        p = val < a[p].val ? a[p].l : a[p].r;
    }

    return a[ans].val;
}

int getNext(int val) {
    int ans = 2; // 无穷大
    int p = root;
    while (p) {
        if (val == a[p].val) {
            if (a[p].r > 0) {
                p = a[p].r;
                while (a[p].l > 0) p = a[p].l; // 右子树上一直向左走
                ans = p;
            }
            break;
        }

        if (a[p].val > val && a[p].val < a[ans].val) ans = p;
        p = val < a[p].val ? a[p].l : a[p].r;
    }

    return a[ans].val;
}

int main() {
    build();

    cin >> n;
    while (n--) {
        int op, x;
        scanf("%d%d", &op, &x);

        switch (op) {
            case 1 : insert(root, x); break;
            case 2 : remove(root, x); break;
            case 3 : printf("%d\n", getRankByVal(root, x) - 1); break;
            case 4 : printf("%d\n", getValByRank(root, x + 1)); break;
            case 5 : printf("%d\n", getPre(x)); break;
            case 6 : printf("%d\n", getNext(x)); break;
        }
    }

    return 0;
}

参考

《算法竞赛进阶指南》 https://en.wikipedia.org/wiki/Random_binary_tree https://medium.com/carpanese/a-