ST表¶
前置知识¶
倍增思想,二进制,对数
目标¶
了解 ST表的基本实现原理,会做模板题
What¶
RMQ问题(Range Maximum/Minimum Query),就是区间最值问题。
ST表(Sparse Table)是其中的一个算法。
Why¶
ST表是用于解决 可重复贡献问题 的数据结构。
给定一个长度为 n 的 序列,经过 \(O(nlogn)\)的预处理后,以 \(O(1)\) 的时间复杂度,在线回答 \([l, r]\) 区间的最值是多少。
ST表能维护的信息非常有限,不能较好地扩展,并且不支持修改操作。
How¶
1、预处理¶
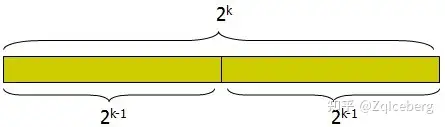
// dp[i][j]表示数列在[i, i + 2 ^ j - 1]里的最大值
// 初始状态是 dp[i][0] = a[i]
// 递推公式 dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1])
void ST_prework(){
for (int i = 1; i <= n; i++) dp[i][0] = a[i];
int Log = (int)log2(1.0 * n) + 1;
for (int j = 1; j < Log; j++)
for (int i = 1; i <= n - (1 << j) + 1; i++)
dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
}
2、查询¶
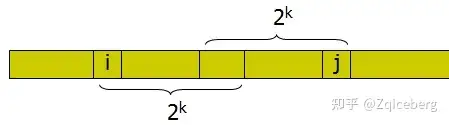
// 询问时,
// 先计算出使得2^k 小于区间长度,且最大
// 那么,就可以用 "从 l 开始的2^k个数" 和 "以 r 结尾的2^k个数",这两段覆盖整个区间 [l, r]
// 即使有重叠也没关系
int ST_query(int l, int r){
int k = (int)log2(1.0 * (r - l + 1));
return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}
3、什么是可重复贡献问题?¶

4、关于log的预处理¶
1、使用cmath的log函数,执行效率很高,影响不大。需要注意的是,参数和返回值都是double
double log (double x);
2、手动预处理
int Log[N]; // 预处理log
Log[1] = 0;
for (int i = 2; i <= n; i++) Log[i] = Log[i >> 1] + 1;
P3865 【模板】ST 表¶
题目链接:https://www.luogu.com.cn/problem/P3865
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], dp[N][20];
int n, m;
void ST_prework(){
for (int i = 1; i <= n; i++) dp[i][0] = a[i];
int Log = (int)log2(1.0 * n) + 1;
for (int j = 1; j < Log; j++)
for (int i = 1; i <= n - (1 << j) + 1; i++)
dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
}
int ST_query(int l, int r){
int k = (int)log2(1.0 * (r - l + 1));
return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
ST_prework();
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", ST_query(l, r));
}
return 0;
}
题单¶
总结¶
ST表是一个很好的用来理解倍增思想的一个算法。代码简洁,易用。