最小生成树¶

前置知识¶

建图，并查集，最短路，Dijkstra，结构体

目标¶

掌握Prim, Kruskal代码模板

What¶

A spanning tree of a graph consists of all nodes of the graph and some of the edges of the graph so that there is a path between any two nodes. Like trees in general, spanning trees are connected(连通的) and acyclic(无环). Usually there are several ways to construct a spanning tree.

A minimum spanning tree(最小生成树) is a spanning tree whose weight is as small as possible.

In a similar way, a maximum spanning tree(最大生成树) is a spanning tree whose weight is as large as possible.

Prim’s algorithm 稠密图朴素n^2¶

发音，普里姆算法

Prim’s algorithm is an alternative method for finding a minimum spanning tree. The algorithm first adds an arbitrary node to the tree. After this, the algorithm always chooses a minimum-weight edge that adds a new node to the tree. Finally, all nodes have been added to the tree and a minimum spanning tree has been found.

Prim’s algorithm resembles Dijkstra’s algorithm. The difference is that Dijkstra’s algorithm always selects an edge whose distance from the starting node is minimum, but Prim’s algorithm simply selects the minimum weight edge that adds a new node to the tree.

Let us consider how Prim’s algorithm works in the following graph:

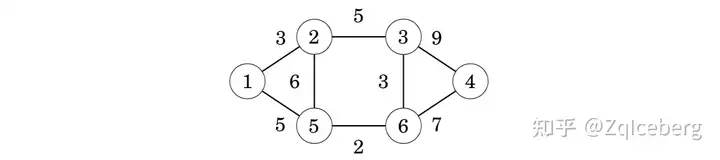
Initially, there are no edges between the nodes:

An arbitrary node can be the starting node, so let us choose node 1. First, we add node 2 that is connected by an edge of weight 3:

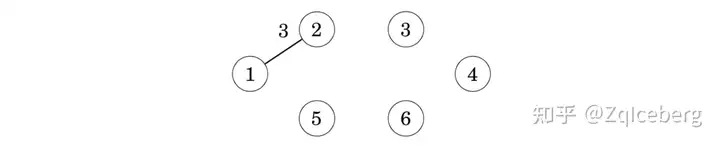
After this, there are two edges with weight 5, so we can add either node 3 or node 5 to the tree. Let us add node 3 first:

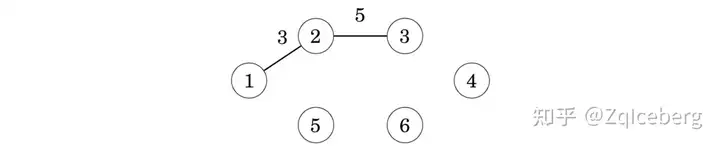
The process continues until all nodes have been included in the tree:

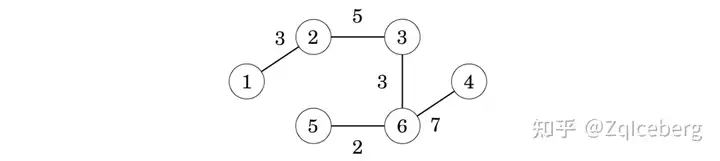
Implementation

Like Dijkstra’s algorithm, Prim’s algorithm can be efficiently implemented using a priority queue. The priority queue should contain all nodes that can be connected to the current component using a single edge, in increasing order of the weights of the corresponding edges.

The time complexity of Prim’s algorithm is *O*(*n*+*m*log*m*)** that equals the time complexity of Dijkstra’s algorithm. In practice, Prim’s and Kruskal’s algorithms are both efficient, and the choice of the algorithm is a matter of taste. Still, most competitive programmers use Kruskal’s algorithm.

OI-Wiki介绍，https://oi-wiki.org/graph/mst/#prim-%E7%AE%97%E6%B3%95(链接有动图)

例题，1349：【例4-10】最优布线问题

# 题意
n个结点，生成MST，最小代价是多少

# 思路
邻接矩阵建图，跑prim，朴素prim

# 代码
#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int g[N][N];
int d[N];
bool vis[N];
int n, res;

void prim()
{
    memset(d, 0x3f, sizeof d);
    for (int i = 0; i < n; i++){
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!vis[j] && (t == -1 || d[j] < d[t]))
                t = j;

        if (i) res += d[t];
        for (int j = 1; j <= n; j++)
            d[j] = min(d[j], g[t][j]);

        vis[t] = true;
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) cin >> g[i][j];

    prim();

    cout << res << '\n';

    return 0;
}

Kruskal’s algorithm 稀疏图 mlogm¶

发音，克鲁斯卡尔算法

In Kruskal’s algorithm, the initial spanning tree only contains the nodes of the graph and does not contain any edges. Then the algorithm goes through the edges ordered by their weights, and always adds an edge to the tree if it does not create a cycle.

The algorithm maintains the components of the tree. Initially, each node of the graph belongs to a separate component. Always when an edge is added to the tree, two components are joined. Finally, all nodes belong to the same component, and a minimum spanning tree has been found.

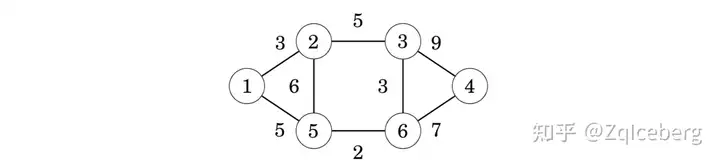
The first step of the algorithm is to sort the edges in increasing order of their weights. The result is the following list:

After this, the algorithm goes through the list and adds each edge to the tree if it joins two separate components.Initially, each node is in its own component:

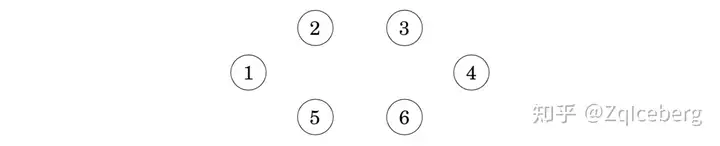
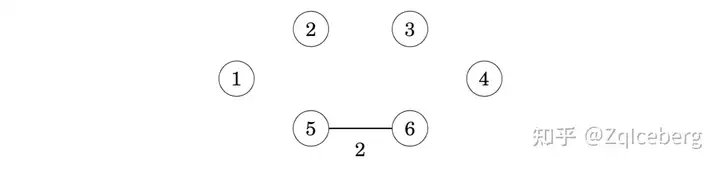
The first edge to be added to the tree is the edge 5–6 that creates a component {5,6} by joining the components {5} and {6}.

After this, the edges 1–2, 3–6 and 1–5 are added in a similar way.

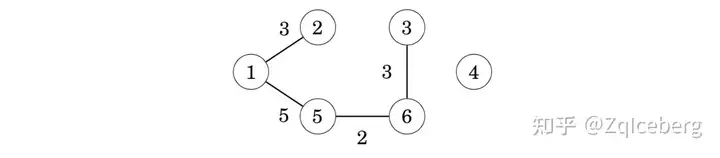
After those steps, most components have been joined and there are two components in the tree: {1,2,3,5,6} and {4}.

The next edge in the list is the edge 2–3, but it will not be included in the tree, because nodes 2 and 3 are already in the same component. For the same reason, the edge 2–5 will not be included in the tree.

Finally, the edge 4–6 will be included in the tree:

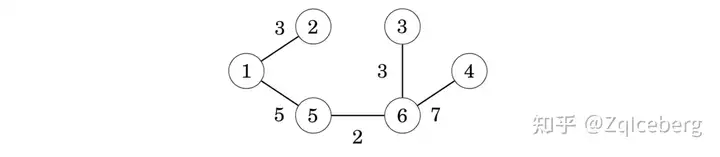
After this, the algorithm will not add any new edges, because the graph is connected and there is a path between any two nodes. The resulting graph is a minimum spanning tree with weight 2+3+3+5+7=20.

Why does this work?

It is a good question why Kruskal’s algorithm works. Why does the greedy strategy guarantee that we will find a minimum spanning tree?

Let us see what happens if the minimum weight edge of the graph is not included in the spanning tree. For example, suppose that a spanning tree for the previous graph would not contain the minimum weight edge 5–6. We do not know the exact structure of such a spanning tree, but in any case it has to contain some edges. Assume that the tree would be as follows:

However, it is not possible that the above tree would be a minimum spanning tree for the graph. The reason for this is that we can remove an edge from the tree and replace it with the minimum weight edge 5–6. This produces a spanning tree whose weight is smaller:

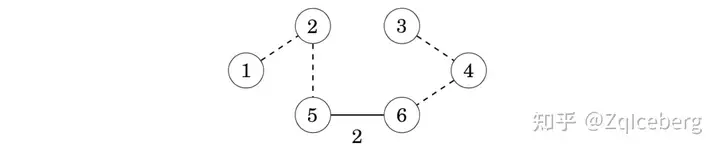
For this reason, it is always optimal to include the minimum weight edge in the tree to produce a minimum spanning tree. Using a similar argument, we can show that it is also optimal to add the next edge in weight order to the tree, and so on. Hence, Kruskal’s algorithm works correctly and always produces a minimum spanning tree.

Implementation

When implementing Kruskal’s algorithm, it is convenient to use the edge list representation of the graph. The first phase of the algorithm sorts the edges in the list in *O*(*m*log*m*)** time. After this, the second phase of the algorithm builds the minimum spanning tree as follows:

for (...) {
  if (!same(a,b)) unite(a,b);
}

We will solve the problem using a union-find structure that implements both functions in O*(log *n*) time. Thus, the time complexity of Kruskal’s algorithm will be *O*(*m* log *n*)* after sorting the edge list.

此处，O(mlogm), O(mlogn)都是对的

例题，1392：繁忙的都市(city)

# 题意
无向图，n个结点，生成MST，输出MST有几条边，输出MST中最大权值的边权

# 思路
跑Kruscal，mlogm

# 代码
#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

struct node
{
    int a, b, w;

    node(int _a = 0, int _b = 0, int _w = 0): a(_a), b(_b), w(_w){}

    bool operator< (const node& W)const{
        return w < W.w;
    }
}edge[N];

int n, m, p[310];

int find(int x)
{
    if (p[x] != x) return p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edge[i] = node(a, b, c);
    }

    sort(edge, edge + m);
    for (int i = 1; i <= n; i++) p[i] = i;

    int cnt = 0, maxn = 0;
    for (int i = 0; i < m; i++){
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;
        int pa = find(a), pb = find(b);
        if (pa != pb){
            p[pa] = pb;
            cnt++;
            maxn = max(maxn, w);
        }
    }

    printf("%d %d\n", cnt, maxn);

    return 0;
}