跳转至

最近公共祖先（LCA）

前置知识

对二进制的理解，倍增思想，树的遍历

What

给定一颗有根树，若结点 z 既是结点 x 的祖先，也是结点 y 的祖先，则称 z 是 x, y 的公共祖先。在 x, y 的公共祖先中，深度最大的一个称为 x, y 的最近公共祖先，记为 LCA(x, y)。

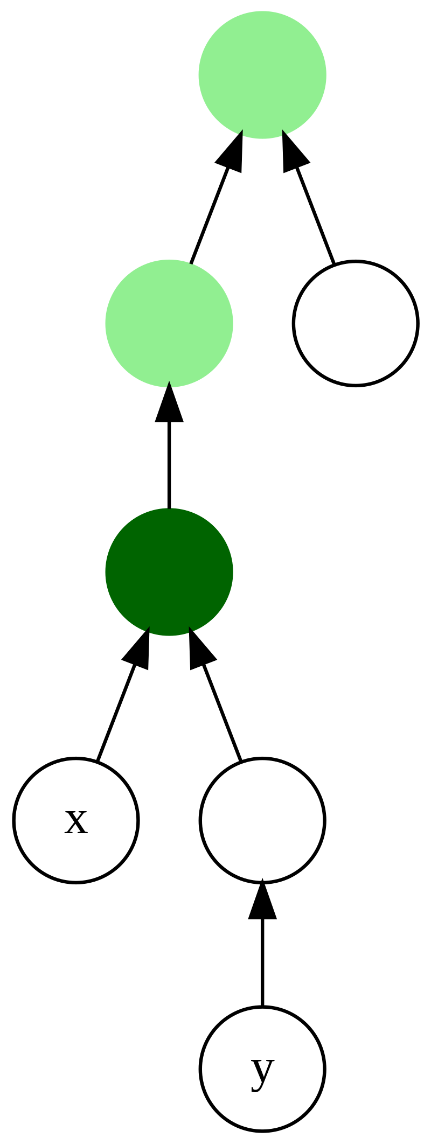
image-20240703175608178

在上图中，x 与 y 的最近公共祖先被标记为深绿色，其他公共祖先被标记为浅绿色

LCA(x, y) 是 x 到根的路径与 y 到根的路径的交会点。它也是 x 与 y 之间的路径上深度最小的结点。

向上标记法

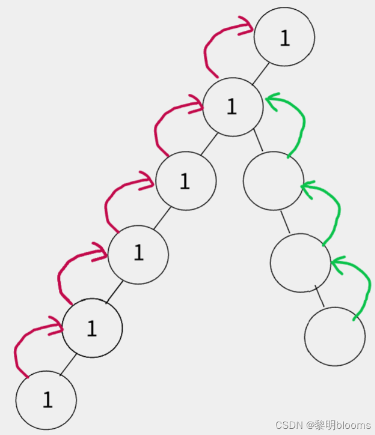
从 x 向上走到根结点，并标记所有经过的结点。

从 y 向上走到根结点，当第一次遇到已标记的结点时，就找到了 LCA(x, y)。

对于每个询问，向上标记法的时间复杂度最坏为 \(O(n)\)。

image-20240703180206266

树上倍增法

树上倍增法，每次向上跳跃的时候，按 2 的幂次进行跳跃，每次跳跃按照幂次递减的步数去跳跃。

我们需要预处理一个 F[x, k] 数组，表示 x 的 \(2^k\) 辈祖先，即从 x 向根结点走 \(2^k\) 步到达的结点。

例如，F[x, 0] 是 x 的父节点，F[x, k] = F[F[x, k - 1], k - 1]。

算法步骤：

  1. 设 d[x] 表示 x 的深度。不妨设 \(d[x] \geq d[y]\)（否则进行交换）。
  2. 用二进制拆分思想，把 x 向上调整到与 y 同一深度（依次尝试从 x 向上走 \(k = 2^{logn},...,2^1,2^0\) 步，检查到达的结点是否比 y 深。在每次检查中，若是，则令 x = F[x, k]，进行迭代向上跳跃）。
  3. 若此时 x = y，说明已经找到了 LCA，LCA 就等于 y。
  4. 用二进制拆分思想，把 x, y 同时向上调整，并保持深度一致且二者不相会（依次尝试把 x, y 同时向上走 \(k = 2^{logn},...,2^1,2^0\) 步，在每次尝试中，若 F[x, k] != F[y, k]，就是为相会，则令 x = F[x, k], y = F[y, k]）。
  5. 此时，x, y 必定只差一步就相会了，它们的父节点 F[x, 0] 就是 LCA。

预处理过程，时间复杂度为 \(O(nlogn)\)，每次查询的时间复杂度为 \(O(logn)\)。

P3379 【模板】最近公共祖先（LCA）

题目链接：https://www.luogu.com.cn/problem/P3379

#include <bits/stdc++.h>

using namespace std;

const int N = 5e5 + 10;

int n, m, s;
vector<int> h[N];
int f[N][20], d[N];
int Log;

void bfs() {
    queue<int> q;
    q.push(s); d[s] = 1;
    while (!q.empty()) {
        int t = q.front(); q.pop();
        for (auto i : h[t]) {
            if (d[i]) continue;

            d[i] = d[t] + 1;
            f[i][0] = t;

            for (int j = 1; j <= Log; j++)
                f[i][j] = f[f[i][j - 1]][j - 1];

            q.push(i);
        }
    }
}

int lca(int x, int y) {
    if (d[x] > d[y]) swap(x, y);
    for (int i = Log; i >= 0; i--)
        if (d[f[y][i]] >= d[x]) y = f[y][i];

    if (x == y) return y;
    for (int i = Log; i >= 0; i--)
        if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];

    return f[x][0];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m >> s;
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        h[x].push_back(y); h[y].push_back(x);
    }

    Log = (int)(log(n) / log(2)) + 1;
    bfs();

    while (m--) {
        int a, b;
        cin >> a >> b;
        cout << lca(a, b) << '\n';
    }

    return 0;
}

题单

参考