跳转至

zqiceberg.com

二叉树

二叉树¶

前置知识¶

数字，结构体，DFS，BFS

目标¶

二叉树的定义，性质，前序/中序/后序遍历

What¶

树是一种非线性数据结构，能很好地描述数据的层次信息。二叉树(Binary Tree, BT)是一种特殊的树型结构，每个结点最多有两个子节点。

二叉树的递归定义如下：二叉树要么为空，要么由根结点(root)、左子树(left subtree)、右子树(right subtree)组成，而左子树和右子树分别是一颗二叉树。

二叉树的 5 种基本形态 1、空二叉树 2、仅有根结点的二叉树 3、右子树为空的二叉树 4、左右子树均非空的二叉树 5、左子树为空的二叉树

性质¶

二叉树的存储方法¶

// 链式存储结构
struct node{
    int data;
    node *lchild, *rchild;  //左儿子，右儿子
};

node *root;


// 顺序存储结构
const int N = 110;
int data[N]；
int lchild[N], rchild[N];   // int child[N][2]; 也可以这样写
int root;

// 完全二叉树的数组表示法
对于完全二叉树，只要确定了结点个数为 n，完全二叉树的形态也就确定了。
对于结点 x，它的左儿子是 2x，右儿子是 2x+1，父亲是 x / 2
无需存储任何和树的形态有关的信息，只需要用一个一维数组就可以表示每个结点上的信息。（优美）

二叉树的递归遍历¶

先序遍历

void dfs(int u) {
    if (u) {
        cout << u;
        dfs(lchild[u]);
        dfs(rchild[u]);
    }
}

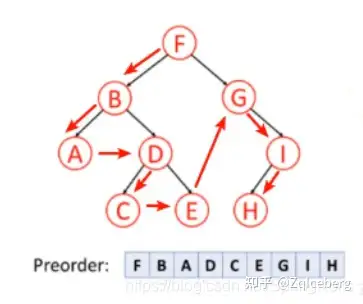
中序遍历

void dfs(int u) {
    if (u) {
        dfs(lchild[u]);
        cout << u;
        dfs(rchild[u]);
    }
}

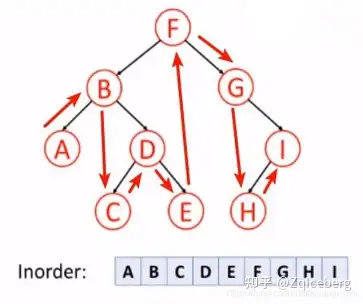
后序遍历

void dfs(int u) {
    if (u) {
        dfs(lchild[u]);
        dfs(rchild[u]);
        cout << u;
    }
}

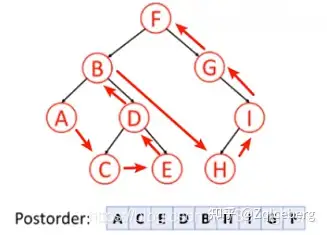
反推

已知中序遍历序列和另外一个序列可以求第三个序列。

前序的第一个是 root，后序的最后一个是 root。
先确定根节点，然后根据中序遍历，在根左边的为左子树，根右边的为右子树。
对于每一个子树可以看成一个全新的树，仍然遵循上面的规律。

已知先序和中序，可以确定出二叉树已知中序和后序，可以确定出二叉树已知先序和后序，不可以确定出二叉树

例题¶

写出下图的前缀表示、中缀表示、后缀表示¶

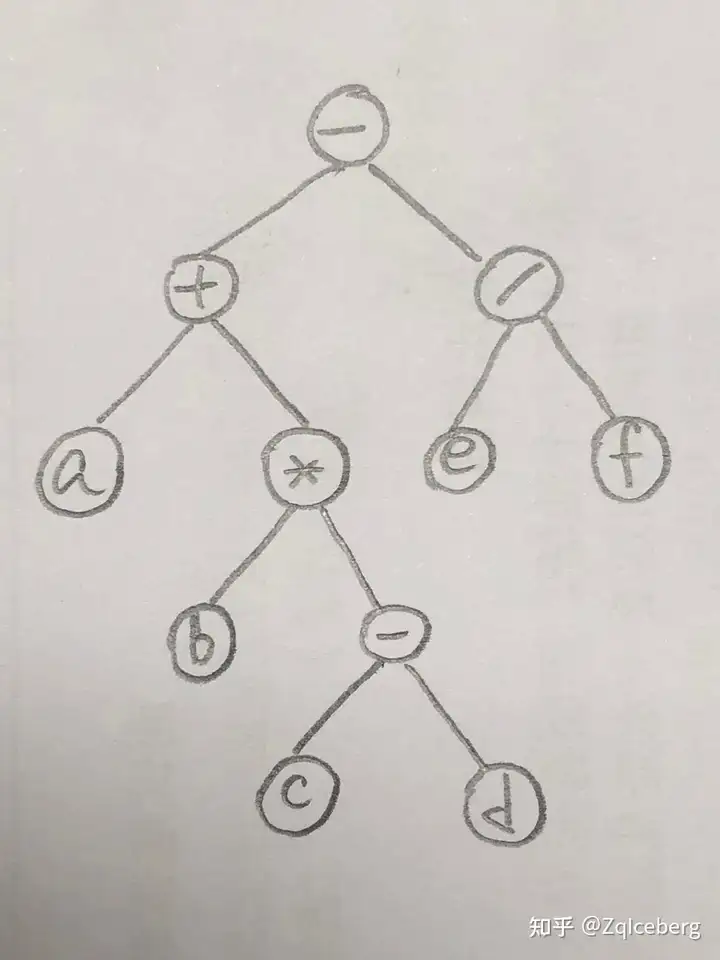
有二叉树中序序列为ABCEFGHD，后续序列为ABFHGEDC，请画出此二叉树，并求前序序列。¶

图画

例题，1339：【例3-4】求后序遍历 ¶

题意：给出先序和中序，求后序

#include <bits/stdc++.h>

using namespace std;

string a, b;

void dfs(int l1, int r1, int l2, int r2)
{
    int root = b.find(a[l1]);

    if (l2 < root) dfs(l1 + 1, l1 + (root - l2), l2, root - 1); //左子树
    if (root < r2) dfs(l1 + 1 + (root - l2), r1, root + 1, r2); //右子树
    cout << a[l1];                                              //后续遍历
}

int main()
{
    cin >> a >> b;
    dfs(0, (int)a.size() - 1, 0, (int)b.size() - 1);
    puts("");

    return 0;
}

例题，1365：FBI树(fbi)¶

题意：全0输出B，全1输出I，既含0又含1输出F

#include <bits/stdc++.h>

using namespace std;

string s;

void dfs(int u, int len){
    if (len == 1){
        if (s[u] == '1') cout << 'I';
        else if (s[u] == '0') cout << 'B';
        return ;
    }

    dfs(u, len / 2);
    dfs(u + len / 2, len / 2);

    // 输出根
    int one = 0, zero = 0;
    int i = u, t = len;
    while (t--) 
        if (s[i] == '1') one++, i++;
        else zero++, i++;

    if (zero == 0 && one) cout << 'I';
    else if (one == 0 && zero) cout << 'B';
    else cout << 'F';
}

int main(){
    int n;
    cin >> n;
    cin >> s;

    dfs(0, 1 << n);
    puts("");

    return 0;
}

题单¶

总结¶

在这里，我们要记住二叉树的几个性质，前序中序后序遍历的经典例题代码