栈 表达式

前置知识

一维数组、stack

目标

利用栈解决表达式求值的问题

What

栈是一种线性数据结构 支持两种基本操作：进栈、出栈 栈的修改与访问，是按照先进后出的原则进行

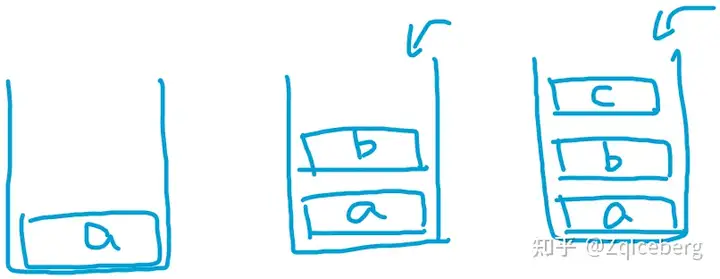
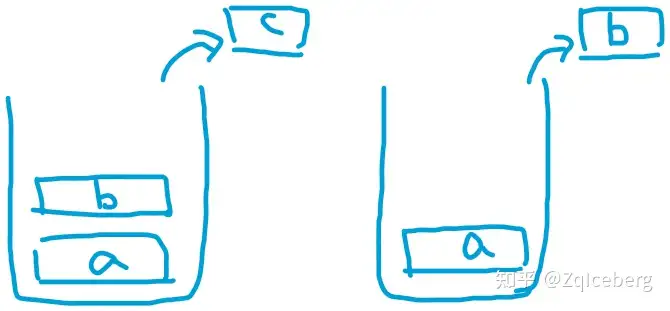
Why

栈的应用：回溯、递归、深度优先搜索

How

用数组模拟栈

// 0 入栈
// 1 出栈
// 2 输出栈顶

#include <bits/stdc++.h>

using namespace std;

int stk[110], tt;
int n, op, x;

int main() {
    cin >> n;
    while (n--) {
        cin >> op;

        if (op == 0) {cin >> x; stk[++tt] = x;}
        if (op == 1 && op > 0) tt--;
        if (op == 2 && op > 0) cout << stk[tt] << '\n';
    }

    return 0;
}

用STL中的栈

// 0 入栈
// 1 出栈
// 2 输出栈顶

#include <bits/stdc++.h>

using namespace std;

stack<int> stk;
int n, op, x;

int main() {
    cin >> n;
    while (n--) {
        cin >> op;

        if (op == 0) {cin >> x; stk.push(x);}
        if (op == 1 && !stk.empty()) stk.pop();
        if (op == 2 && !stk.empty()) cout << stk.top() << '\n';
    }

    return 0;
}

经典例题

例题，表达式括号匹配(stack)

题意，检查表达式中的左右括号是否匹配 思路，用一个栈维护左括号和右括号的关系，右括号，没有左括号配对就是非法。左括号，最后没有右括号配对就是非法

#include <bits/stdc++.h>

using namespace std;

string s;
stack<char> stk;

int main()
{
    cin >> s;

    bool flag = false;
    for (int i = 0, len = s.size(); i < len; i++){
        if (s[i] == '@') break; 

        if (s[i] == '(') stk.push(s[i]);
        if (s[i] == ')'){
            //栈是空的
            //栈非空，有(可以配对
            if (stk.empty()){flag = true; break;}

            stk.pop();
        }
    }

    if (flag || !stk.empty()) cout << "NO" << '\n';
    else cout << "YES" << '\n';

    return 0;
}

例题，后缀表达式的值

题意，给你一个后缀表达式，求值。表达式中没有括号，只有加减乘除 思路，用一个栈维护数字，用一个栈维护运算符

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

string s;
stack<LL> num;
stack<char> op;
int len;
map<char, int> mp;

bool check_num(char c){
    if (c >= '0' && c <= '9') return true;
    return false;
}

void calc()
{
    LL y = num.top(); num.pop();
    LL x = num.top(); num.pop();
    if (op.top() == '+') num.push(x + y);
    if (op.top() == '-') num.push(x - y);
    if (op.top() == '*') num.push(x * y);
    if (op.top() == '/') num.push(x / y);

    op.pop();
}

int main()
{
    getline(cin, s);
    len = s.size();
    for (int i = 0; i < len; i++){
        if (s[i] == '@') break;

        if (check_num(s[i])){
            int j = i;
            LL t = 0;
            while (check_num(s[j])){
                t = t * 10 + (s[j] - '0');
                j++;
            }
            num.push(t);
            i = j;
        }
        else{
            if (!op.empty()){
                calc();
            }
            op.push(s[i]);
        }
    }

    while (!op.empty()) calc();
    cout << num.top() << '\n';

    return 0;
}

例题，表达式求值

题意，给你一个中缀表达式，只包含加法、乘法，没有括号。求表达式的值 思路，一个数字栈，一个符号栈，用一个map维护运算符优先级

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll mod = 10000;

string s;
stack<char> op;
stack<ll> num;
map<char, int> mp;

void calc(){
    char c = op.top(); op.pop();
    ll a = num.top(); num.pop();
    ll b = num.top(); num.pop();
    if (c == '+') num.push((a + b) % mod);
    if (c == '-') num.push((a - b) % mod);
    if (c == '*') num.push((a * b) % mod);
}

int main(){
    cin >> s;

    mp['+'] = 0, mp['-'] = 0, mp['*'] = 1, mp['/'] = 1;
    for (int i = 0, len = s.size(); i < len; i++){
        if (s[i] == '*' || s[i] == '/') op.push(s[i]);
        else if (s[i] == '+' || s[i] == '-'){
            while (!op.empty() && mp[op.top()] > mp[s[i]]) calc();

            op.push(s[i]);
        }
        else{
            ll t = 0;
            int j = i;
            while (j < len && s[j] >= '0' && s[j] <= '9') t = t * 10 + (s[j++] - '0');
            num.push(t % mod);
            i = j - 1;
        }
    }

    while (!op.empty()) calc();

    cout << num.top() << '\n';

    return 0;
}

例题，中缀表达式值(expr)

题意，给你一个中缀表达式，合法就求值，不合法输出NO 思路，一个数字栈，一个符号栈，一个括号栈（用来处理括号合法性） 此题适合提升代码能力，要反复练习

#include <bits/stdc++.h>

using namespace std;

string s;
stack<int> num;
stack<char> op, brackets; //brackets用来判断括号的合法性
map<char, int> mp;
bool flag;

void init()
{
    mp['+'] = 1, mp['-'] = 1;
    mp['*'] = 2, mp['/'] = 2;
}

void calc()
{
    int y = num.top(); num.pop();
    int x = num.top(); num.pop();
    char c = op.top(); op.pop();

    int res = 0;
    if (c == '+') res = x + y;
    if (c == '-') res = x - y;
    if (c == '*') res = x * y;
    if (c == '/') res = x / y; //未判断除数是0的问题

    num.push(res);
}

bool check_num(char c)
{
    if (c >= '0' && c <= '9') return true;
    return false;
}

int main()
{
    init();

    cin >> s;

    if (s[0] == '*' || s[0] == '/' || s[0] == '+' || s[0] == ')'){ //上来就运算符号,是bug
        cout << "NO" << '\n';
        return 0;
    }

    for (int i = 0, len = (int)s.size(); i < len; i++){
        if (s[i] == '@') break;

        if (i == 0 && s[i] == '-'){
            int t = 0;
            int j = i + 1;
            while (j < len && check_num(s[j])){
                t = t * 10 + (s[j] - '0');
                j++;
            }

            num.push(-t);
            i = j - 1;
            continue;
        }

        if (check_num(s[i]))
        {
            int t = 0;
            int j = i;
            while (j < len && check_num(s[j])){
                t = t * 10 + (s[j] - '0');
                j++;
            }
            num.push(t);
            i = j - 1;
        }
        else if (s[i] == '('){
            op.push('('); brackets.push('(');
        }
        else if (s[i] == ')'){
            if (brackets.empty()){flag = true; break;}

            while (op.top() != '('){ //把括号里面的都计算干净
                calc();
            }

            op.pop(); brackets.pop(); //弹出左括号
        }
        else{
            if (mp.count(s[i]) && mp.count(s[i-1])){ //两个运算符号连在一块，是bug
                flag = true;
                break;
            }

            while (!op.empty() && mp[op.top()] >= mp[s[i]]){
                calc();
            }

            op.push(s[i]);
        }
    }

    while (!op.empty() && !flag){
        if (op.top() == '('){flag = true; break;} //有多余的(

        calc();
    }

    if (flag) cout << "NO" << '\n';
    else cout << num.top() << '\n';

    return 0;
}

总结

表达式括号匹配(stack)，只判断括号是否匹配 后缀表达式的值，给你的是后缀，但也需要用getline读入，拆数字 表达式求值，给你的中缀表达式，一个字符串读入，也需要拆数字，需要处理运算符优先级 中缀表达式值(expr)，还要判断表达式的合法性，最麻烦，但也最锻炼人

参考

https://oi-wiki.org/ds/stack/