跳转至

排序算法

前置知识

数组，sort()，前缀和

目标

基础排序算法，算法原理，代码模板，算法思想应用

What

使用场景：Given an array that contains n elements, your task is to sort the elements in increasing order

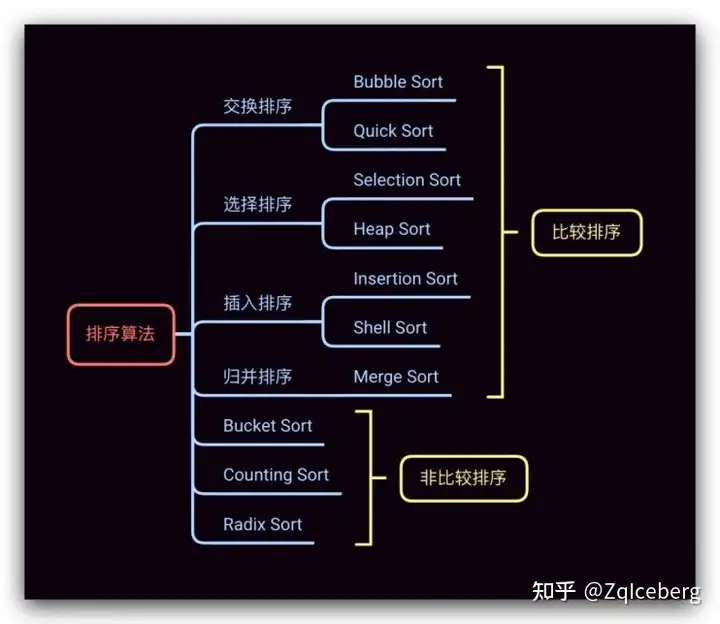
分类：比较排序，非比较排序。

  • 比较排序，就是基于比较的排序，代码中一定有一个比较的动作。
  • 非比较排序，就是代码中没有if判断大小的行为，不是用比较来确定排序顺序的。

排序算法，有很多，并且程序员面试笔试题目中，有很多排序算法的深入理解的考察。

在NOIP竞赛中，优先掌握冒泡、选择、插入、归并、快排、计数的代码实现和原理应用，掌握时间复杂度的判断，掌握稳定的概念。

img

sort()函数

#include <bits/stdc++.h>

using namespace std;

vector<int> A;

int main() {
    A.push_back(2);
    A.push_back(1);
    A.push_back(3);

    sort(A.begin(), A.end());
    for (auto x : A) cout << x << ' ';
    puts("");

    return 0;
}

#include <bits/stdc++.h>

using namespace std;

vector<int> A;

int main() {
    A.push_back(2);
    A.push_back(1);
    A.push_back(3);

    sort(A.begin(), A.end(), greater<int>());  // 从大到小
    for (auto x : A) cout << x << ' ';
    puts("");

    return 0;
}

#include <bits/stdc++.h>

using namespace std;

int a[110], n;

int main() {
    a[0] = 2, a[1] = 1, a[2] = 3;
    n = 3;

    sort(a, a + n); // [0, n) 左闭右开区间
    for (int i = 0; i < n; i++) cout << a[i] << ' ';
    puts("");

    return 0;
}

#include <bits/stdc++.h>

using namespace std;

int a[110], n;

int main() {
    a[0] = 2, a[1] = 1, a[2] = 3;
    n = 3;

    sort(a, a + n, greater<int>());  // 从大到小
    for (int i = 0; i < n; i++) cout << a[i] << ' ';
    puts("");

    return 0;
}

#include <bits/stdc++.h>

using namespace std;

int a[110], n;

int main() {
    a[1] = 2, a[2] = 1, a[3] = 3;
    n = 3;

    sort(a + 1, a + 1 + n, greater<int>()); // 如果数组的下标是从1开始的，那么要这样写 [1, n + 1) 左闭右开区间
    for (int i = 1; i <= n; i++) cout << a[i] << ' ';
    puts("");

    return 0;
}

冒泡排序，比较排序，稳定

Bubble Sort（冒泡排序）是一种简单直观的排序算法。

它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。

遍历数列的工作是重复地进行，直到没有再需要交换，也就是说该数列已经排序完成。

冒泡排序，排序n轮，每一轮遍历一遍数组。当发现两个连续数字顺序不对时，交换他们。

如果是正序排列，每一次 swap，减少一个逆序对

所以，冒泡排序，进行了几次 swap，就可以判断数列中有多少个逆序对

img

void bubble_sort01(){
    for (int i = 0; i < n; i++)               //枚举有几趟冒泡
        for (int j = 0; j < n - 1; j++)
            if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);
}

// 冒泡排序有很多优化版本，这里仅掌握最简单的

选择排序，比较排序，不稳定

首先在未排序序列中找到最小（最大）元素，存放到排序序列的起始位置

再从剩余未排序元素中继续寻找最小（最大）元素，然后放到已排序序列的末尾

重复第二步，直到所有元素均排序完毕

为什么不稳定呢？（此处一定要会举例证明）

例如：

5 3 5 2 4

第一趟排序，第 1 个 5 和 2 发生交换

2 3 5 5 4

但是，这样两个 5 的先后顺序发生了改变。所以，不稳定。

img

void selection_sort(){
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++)          //枚举未排序的部分
            if (a[j] < a[i]) swap(a[j], a[i]);   //把最小的交换到a[i]上
}

插入排序，比较排序，稳定

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。

如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面（所以稳定）。

插入排序，插在哪个位置，其实是一个遍历的过程，这个遍历是就近遍历，遍历到合适的位置，就会停下来。

如果是一个已经排好序的序列，更改了某一个值，想要快速的得到新的序列，那么可以对变更的值，进行向左找位置，向右找位置，\(O(n)\)的时间或者更小，完成新的排序（《【21CSPJ普及组】插入排序》）

img

void insertion_sort(){
    for (int i = 1; i < n; i++){   //从第二个数a[1]开始
        int t = a[i];

        int j = i - 1;
        while (j >= 0 && a[j] > t){
            a[j + 1] = a[j];      //依次往后坐一位
            j--;
        }

        a[j + 1] = t;             //跳出while时，j指向的是第一个a[j]<=t的位置
    }
}

快速排序，比较排序，不稳定

算法步骤：

选一个基准 pivot，一般是 int mid = (l + r) / 2; （\(pivot\) 英[ˈpɪvət] 中心点）

把比 mid小的，放到左边。把比 mid 大的，放到右边

递归地对左半部分，对右半部分，进行相同的操作

体现了分治思想

img

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[(l + r) >> 1];
    while (i < j)
    {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

归并排序，比较排序，稳定

归并排序，有两个理论基础：

  • 一是将两个有序的序列，合并，可以得到一个有序的序列
  • 二是一个序列只有一个元素，那么这个序列是有序的

算法步骤：

  1. 递归的拆分序列，直到只有一个元素，构造出有序的序列（体现了分治思想）
  2. 回溯的时候合并，合并有序的序列，逐层的得到更长的有序的序列

使用场景：

  • 两个有序的序列，可以 \(O(n)\) 的时间复杂度，合并成一个有序的序列
  • 求逆序对的个数
  • 两两相邻比较，比较完，又要整体排个序。\(O(n)\) 可以考虑合并的方式(《【11NOIP普及组】瑞士轮》)

img

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

计数排序，非比较排序，稳定

计数排序的核心，在于将输入的数据值转化为键存储在额外开辟的数组空间中。

作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

反过来，如果数据范围非常明确，那么很可能是计数排序。

很多教材，把这个算法称为桶排，当然，这不是桶排。稍加思索，就能明辨。

img

image-2024071211521794

counting-sort-animate

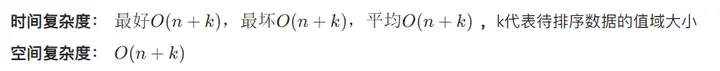
void counting_sort(){
    // cnt[x] 记录x出现的次数
    for (int i = 0; i < n; i++) cnt[a[i]]++;                 

    // 维护出 比x小的有多少个
    // 前置知识：前缀和
    for (int i = 1; i <= maxn; i++) cnt[i] += cnt[i - 1];    

    // b[排第几个] = 原数组中的数值
    // 从后往前拿，cnt从大到小，保证了稳定性
    for (int i = n - 1; i >= 0; i--) b[--cnt[a[i]]] = a[i];  
}

题单

2075：【21CSPJ普及组】插入排序（sort）(名字叫插入排序，但又不是原始的插入排序，多思考)

1938：【07NOIP普及组】奖学金（自定义排序，选择排序，插入排序）

ZqIceberg：CSP 2019 入门组第一轮 计数排序（初赛试题）

2005：【20CSPJ普及组】直播获奖（分析数据范围，分析时间复杂度，确定算法，多思考）

1311：【例2.5】求逆序对

总结

冒泡、选择、插入，\(O(n^2)\)

归并、快排，\(O(nlogn)\)

计数，\(O(n+k)\)

参考

OI-WIKI