递推与递归

前置知识

一维数组，或者要会使用有限个变量，互相传递数值迭代前进的操作

函数理解深入（带参的函数，有返回值的函数，函数自己调用自己）

目标

简单的递推问题，简单的递归问题，会画图分析思考过程。

递推

递推 是程序遍历状态空间的基本方式。

由已知的 “问题边界” 为起点，向 “原问题” 正向推导的扩展方式就是递推。

我们以 \(1+2+3+..+n\) 的问题为例，

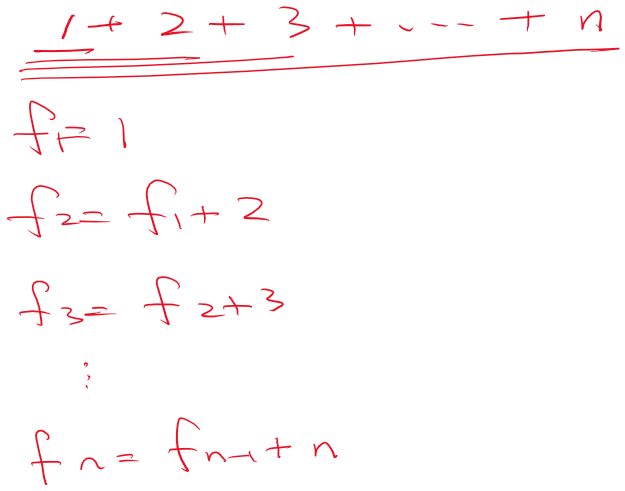
例题，菲波那契数列(2)

题意，多次询问斐波那锲数列第 \(i\) 位的数值是多少

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

int f[N];

void init()
{
    f[1] = 1, f[2] = 1;
    for (int i = 3; i <= N; i++){
        f[i] = f[i - 1] + f[i - 2];
        f[i] %= 1000;
    }
}

int main()
{
    int n;
    cin >> n;

    init();

    while (n--){
        int x;
        scanf("%d", &x);
        printf("%d\n", f[x]);
    }

    return 0;
}

递归

递归是程序遍历状态空间的基本方式。

以“原问题”为起点，尝试寻找把状态空间缩小到已知的“问题边界”的路线。

再通过该路线反向回溯的遍历方式，就是递归。

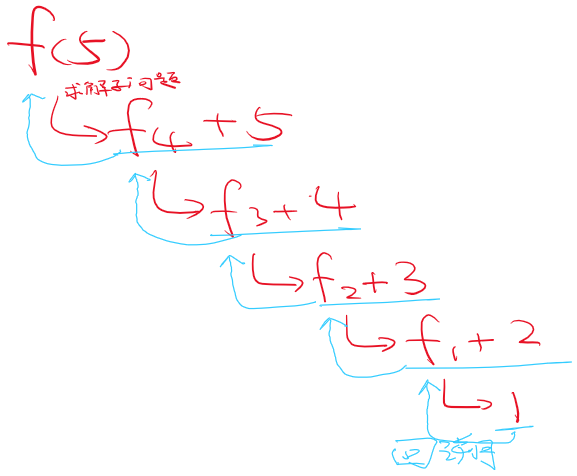
我们以 \(1+2+3+..+n\) 的问题为例，逐渐缩小问题规模，缩小到已知边界，回溯求解的过程

int f(int n) {
    if (n == 1) return 1;

    return f(n - 1) + n;
}

我们以f(5)的执行过程为例，进行分析

例题，菲波那契数列

题意，多次询问斐波那契数列第 \(i\) 位的数值是多少

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

LL f(int n)
{
    if (n == 1) return 1;
    if (n == 2) return 1;

    return f(n - 1) + f(n - 2);
}

int main()
{
    int n;
    cin >> n;

    while (n--){
        int x;
        cin >> x;

        cout << f(x) << '\n';
    }

    return 0;
}

递推题单

菲波那契数列(2)

Pell数列

上台阶

【例3.4】昆虫繁殖

流感传染

放苹果

吃糖果

移动路线

【例3.5】位数问题

【例3.6】过河卒(Noip2002)

递归题单

菲波那契数列

Pell数列

爬楼梯

汉诺塔问题

放苹果

【例4.5】集合的划分

分解因数

【例4.6】数的计数(Noip2001)

求最大公约数问题

分数求和

因子分解

判断元素是否存在

扩号匹配问题

逆波兰表达式

2的幂次方表示

总结

递归，是第一个难关。可能有很长时间，不能理解递归的执行过程，这是正常的。

重点要记住并反复理解，递归的代码框架。