基数排序

前置知识

计数排序

目标

算法思想，代码模板

基数排序，非比较排序，稳定

基数排序（Radix sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

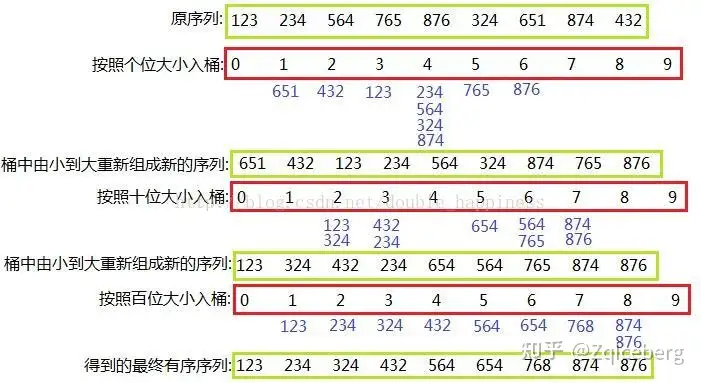
它是这样实现的：

1. 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零
2. 然后，从最低位开始，依次进行一次排序
3. 这样从最低位排序一直到最高位排序完成以后
4. 数列就变成一个有序序列

动图演示：

静图演示：

最坏时间复杂度，\(O(k *n)\)，其中 \(n\) 是排序元素的个数，\(k\) 是数字位数

空间复杂度，\(O(k + n)\)

\(k\) 决定了进行多少轮处理，而 \(n\) 是每轮处理的操作数目。

代码模板

// n个数，每个数有k个关键字
// 对这n个数，进行k个关键字排序

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, k;       //n个数，每个数有k个关键字
int maxn = 100; //每个关键字最大是100
int cnt[N];

struct node{
    int key[110]; //模拟100位数

    bool operator< (const node& W)const{
        for (int i = 1; i <= k; i++){
            if (key[i] == W.key[i]) continue;
            return key[i] < W.key[i];
        }

        return false;
    }
}a[N], b[N];

void counting_sort(int p){
    memset(cnt, 0, sizeof cnt);

    for (int i = 0; i < n; i++) cnt[a[i].key[p]]++;
    for (int i = 1; i <= maxn; i++) cnt[i] += cnt[i - 1];

    // 为保证排序的稳定性，此处循环i应从n到1
    // 即当两元素关键字的值相同时，原先排在后面的元素在排序后仍应排在后面
    for (int i = n - 1; i >= 0; i--) b[--cnt[a[i].key[p]]] = a[i];

    memcpy(a, b, sizeof a);
}

void radix_sort(){
    for (int i = k; i >= 1; i--)
        counting_sort(i);
}

int main(){
    cin >> n >> k;

    for (int i = 0; i < n; i++)
        for (int j = 1; j <= k; j++) cin >> a[i].key[j];

    //sort(a, a + n);  //自定义一个快排，模拟数据进行验证
    radix_sort();

    for (int i = 0; i < n; i++){
        for (int j = 1; j <= k; j++) cout << a[i].key[j] << ' ';
        puts("");
    }

    return 0;
}

/*
测试样例
3 3
33 44 55
11 22 33
33 55 66


3 3
33 11 22
11 22 33
88 22 10
*/

总结

基数排序，非比较排序，稳定

\(O(k * n)\)

参考

https://zh.wikipedia.org/wiki/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F