前缀和 差分¶
前置知识¶
数组
目标¶
前缀和思想,一维前缀和、二维前缀和
差分思想,一维差分,二维差分
一维前缀和¶
前缀和可以简单理解为「数列的前项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
利用前缀和可以在常数时间复杂度中查询区间和
例题,P8218 【深进1.例1】求区间和¶
题意,m 次询问,每次输出 [l, r] 的区间和
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], n, m;
long long s[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
cin >> m;
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
printf("%lld\n", s[r] - s[l - 1]);
}
return 0;
}
二维前缀和¶
例题,P1719 最大加权矩形¶
题意,输入最大子矩阵和,n <= 120
#include <bits/stdc++.h>
using namespace std;
const int N = 150;
int a[N][N], s[N][N], n;
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) cin >> a[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
int ret = -2e9;
for (int xa = 1; xa <= n; xa++)
for (int ya = 1; ya <= n; ya++)
for (int xb = xa; xb <= n; xb++)
for (int yb = ya; yb <= n; yb++)
ret = max(ret, s[xb][yb] - s[xa - 1][yb] - s[xb][ya - 1] + s[xa - 1][ya - 1]);
cout << ret << '\n';
return 0;
}
一维差分¶
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
利用差分可以在常数时间复杂度中对序列进行区间操作
前缀和是用元数据求元与元之间的并集关系,而差分则是根据元与元之间的逻辑关系求元数据,是互逆思想

我们对[2, 5]区间上的每一个数,加上1
我们令b[2] += 1, b[5 + 1] -= 1,最后做前缀和,还原出来原数组,就可以了
所以,更改b[i]的值,相当于,对原数组,从第 i 项开始,每一个数字,都加上一个数

例题,P2367 语文成绩¶
题意,每次修改对 [l, r] 区间上的每一个数字增加或者减少,问 m 次修改后,全班的最低分
#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
int n, p;
int a[N], b[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> p;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) b[i] = a[i] - a[i - 1];
while (p--) {
int l, r, z;
cin >> l >> r >> z;
b[l] += z, b[r + 1] -= z;
}
int ret = 110;
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
ret = min(ret, b[i]);
}
cout << ret << '\n';
return 0;
}
二维差分¶
下图中,将中间蓝色矩形中的每个位置都加上一个 c
类似于,容斥原理
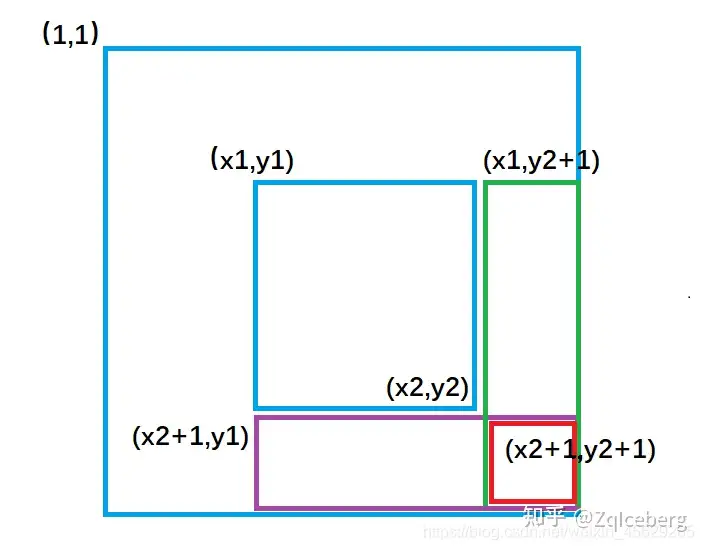
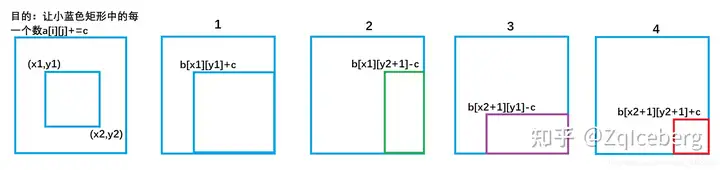
//对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
例题,P3397 地毯¶
题意,n 条地毯,给出每条地毯的左上角和右下角坐标。输出一个矩阵,每个位置上用整数表示这个点被几个地毯覆盖。n <= 1e3
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int b[N][N], n, m;
void insert(int xa, int ya, int xb, int yb, int c) {
b[xa][ya] += c;
b[xb + 1][ya] -= c;
b[xa][yb + 1] -= c;
b[xb + 1][yb + 1] += c;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
while (m--) {
int xa, ya, xb, yb;
cin >> xa >> ya >> xb >> yb;
// construct the inital differential array
insert(xa, ya, xb, yb, 1);
}
// do prefix sum
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) cout << b[i][j] << ' ';
cout << '\n';
}
return 0;
}
例题,输入一个二维数组,对中间的一个区域,加上一个数,然后输出二维数组¶
n 行 m 列的二维数组,对左上角 (x1, y1) 到右下角 (x2, y2) 上的所有数组,加上一个数 x。输出修改后的二维数组
#include <bits/stdc++.h>
using namespace std;
int a[110][110], b[110][110], n, m;
int xa, ya, xb, yb, x;
void insert(int xa, int ya, int xb, int yb, int x) {
b[xa][ya] += x;
b[xa][yb + 1] -= x;
b[xb + 1][ya] -= x;
b[xb + 1][yb + 1] += x;
}
void doPrefixSum() {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
//b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + b[i][j];
}
void print(int a[][110]) {
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++) cout << a[i][j] << ' ';
puts("");
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) cin >> a[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) insert(i, j, i, j, a[i][j]);
cin >> xa >> ya >> xb >> yb >> x;
insert(xa, ya, xb, yb, x);
doPrefixSum();
print(a); // print(b);
return 0;
}
/*
5 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
2 2 4 4 1
*/
更多的差分例题¶
例题,缩进对齐¶
题意,序列 a,要变成序列 b,最少需要几步操作。每次操作可以对一段区间的数值,加减 x
思路,把 a 变成 b,等价于,把 a 的差分数组变成 b 的差分数组。
/*
补充定义,a[0] = a[n + 1] = 0, 差分数组 c[i] = a[i] - a[i - 1]
注意c[1... n+1]的和,刚好是0
对a[1..4]加1,则在,差分数组c[]上的操作是c[1] +1, c[5] - 1
就是每一次操作,差分数组上,都有一个+1,一个-1的,成对出现的操作
即,c[]数组每次的操作效果为,任意选取两个数,一个加1,一个减1
原数组,a[] -> b[]
差分数组,c[] -> d[]
把c[]变成d[],最少需要操作多少次,
只需要维护当 if (c[i] > d[i]) cnt += c[i]-d[i],累加求和
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int a[N], b[N], c[N], d[N]; // c是a的差分数组,d是b的差分数组
int n;
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i] >> b[i];
a[0] = b[0] = a[n + 1] = b[n + 1] = 0;
int ans = 0; //用来记录我们所需要的最小的操作的次数
for (int i = 1; i <= n + 1; i++)
{
c[i] = a[i] - a[i - 1];
d[i] = b[i] - b[i - 1];
if (c[i] >= d[i])
{
ans += c[i] - d[i];
}
}
cout << ans;
return 0;
}
例题,平整序列¶
题意,把序列 a,改成全是 0,最少需要几步操作。每次操作可以对一段区间的数值 +1,或者-1
思路,将序列重新变为 0 就是将差分序列中所有数变为 0,差分变换的时候正负是成对出现的,有 +1 就有 -1,因此只考虑一个方向。
// 缩进对齐
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
int a[N], b[N];
ll ret, n;
int main(){
cin >> n;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n + 1; i++) b[i] = a[i] - a[i - 1];
for (int i = 1; i <= n + 1; i++)
if (b[i] > 0) ret += b[i];
cout << ret << '\n';
return 0;
}
题单¶
一刷:
USACO 2016 Subsequences Summing to Sevens
二刷:
总结¶
做前缀和、差分数组,下标,都必须从 1 开始,否则,代码不好写
参考¶
《深入浅出程序设计竞赛》