初等数论

前置知识

小学数学

目标

算数基本定理，判断质数，分解质因子，GCD，约数个数，约数之和

算数基本定理

判断质数

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i++)
        if (x %i == 0) return false;

    return true;
}

分解质因子

void divide(int x)
{
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0)
        {
            int s = 0;  // 计数器，记录个数
            while (x % i == 0) x /= i, s++;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;

    puts("");
}

欧几里得算法 (GCD)

// 最大公约数
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

// 最小公倍数
lcm = a * b / gcd(a, b);
实际上，不能这样写代码，会溢出！
lcm = a / gcd(a, b) * b;

约数个数

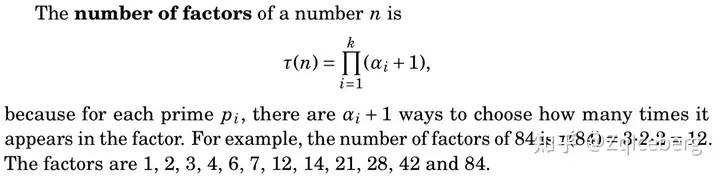
（理论：乘法原理、质因子之间的独立性）

84 = 2^2 * 3^1 * 7^1
t(84) = (2+1) * (1+1) * (1+ 1) = 3 * 2 * 2 = 12（12个约数）

1 2 3 4 6 7 12 14 21 28 42 84， 12个

例题，869. 试除法求约数

#include <bits/stdc++.h>

using namespace std;

set<int> get_divisors(int n) {
    set<int> res;
    for (int i = 1; i <= n / i; i++)
        if (n % i == 0){
            res.insert(i);
            if (i != n / i) res.insert(n / i);
        }

    return res;
}

int main() {
    int n;
    cin >> n;

    while (n--){
        int x;
        cin >> x;

        auto res =  get_divisors(x);

        for (auto t : res) cout << t << ' ';
        cout << endl;
    }

    return 0;
}

例题，870. 约数个数

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;

    map<int, int> primes;
    while (n--) {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i++)
            while (x % i == 0) {
                x /= i;
                primes[i] ++;
            }
        if (x > 1) primes[x]++;
    }

    LL ret = 1;
    for (auto x : primes) {
        int y = x.second;
        ret = ret * (y + 1) % mod;
    }

    cout << ret << endl;

    return 0;
}

约数之和

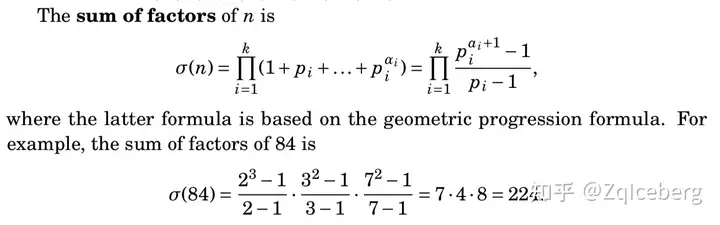
（理论：乘法分配律、质因子之间的独立性、乘法原理、等比数列求和公式）

例题，871. 约数之和

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;

    map<int, int> primes;
    while (n--) {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i++)
            while (x % i == 0) {
                x /= i;
                primes[i]++;
            }

        if (x > 1) primes[x]++;
    }

    LL res = 1;
    for (auto prime : primes) {
        int p = prime.first, a = prime.second;
        LL t = 1;
        while (a--) t = (t * p + 1) % mod; // p^0 + p^1 + ... + p^a

        res = res * t % mod;
    }
    cout << res << endl;

    return 0;
}

题单

869. 试除法求约数 870. 约数个数 871. 约数之和

总结

算数基本定理，判断质数，分解质因子，GCD，约数个数，约数之和 这些是基本的，其他的以专题方式介绍（筛法求质数）