跳转至

快速乘

前置知识

龟速乘，long double

目的

快速乘原理

2009年全国信息学奥林匹克冬令营论文，成都七中，骆可强

image-20240702161411526

关键的话：

我们可以预见其差是一个 64bit 可容纳的正整数，

那么溢出部分的差仅可能为 0 或者 1。

如果溢出部分差为 1，就是负数的情况。

思路，利用 \(a * b \ mod \ p=a*b-\lfloor a * b \ / \ p \rfloor *p\) 。

首先，当 \(a, b < p\) 时，\(a*b \ / \ p\) 向下取整一定小于 \(p\)。

可以利用浮点数执行 \(a*b \ / \ p\) 的运算，而不用关心小数点之后的部分，

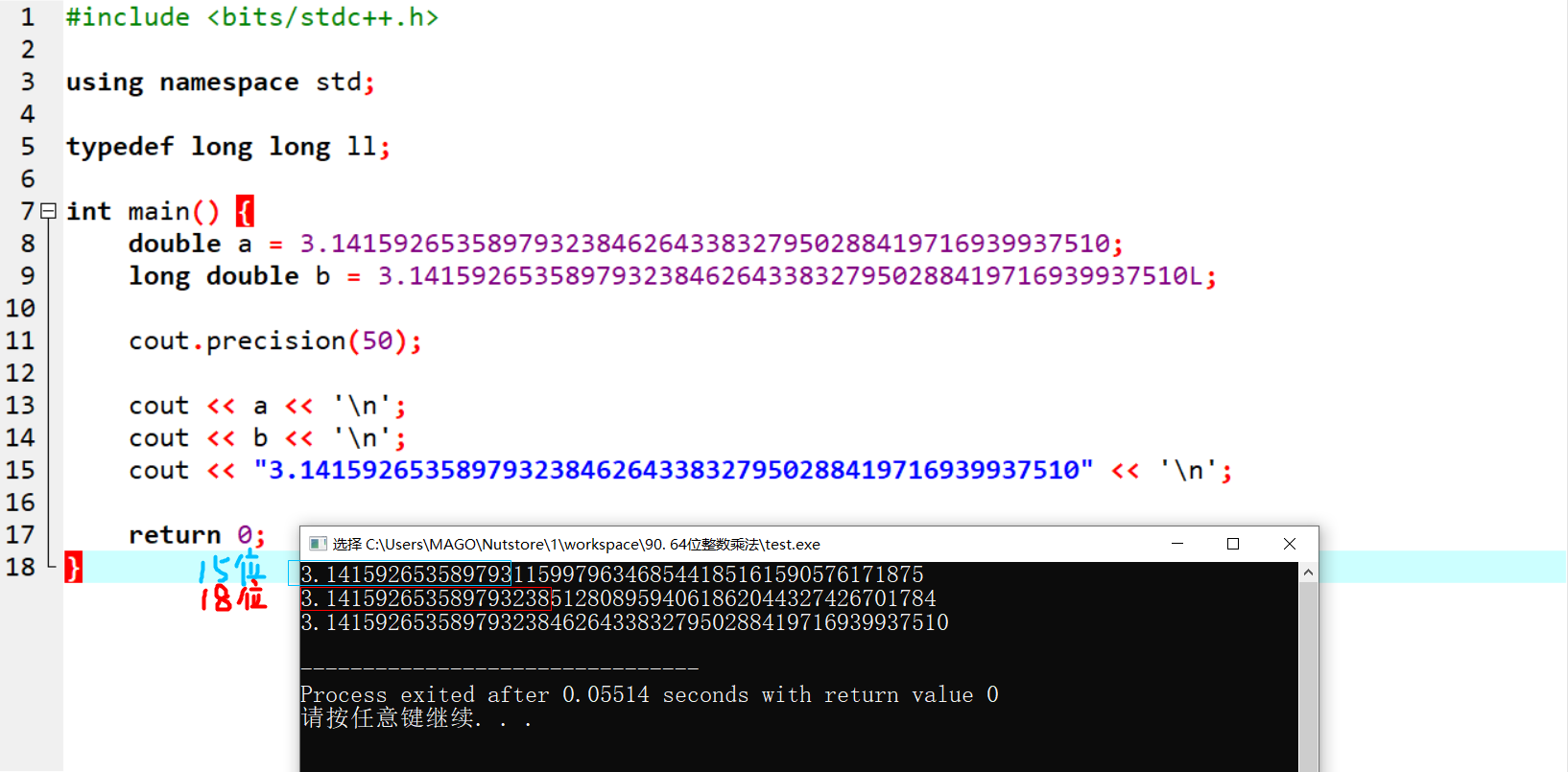
浮点类型 long double 在十进制下的有效数字有 \(18\)~\(19\) 位，足够胜任。

当浮点数的精度不足以保存精确数值时，它会像科学计数法一样舍弃低位，正好符合我们的要求。

虽然浮点数有时会导致精度问题（\(p|a*b\) 时，\(\lfloor a * b \ / \ p \rfloor\) 会比实际少 1），但此时，\(p | (a*b-\lfloor a * b \ / \ p \rfloor *p)\)。

取模之后，结果仍然是 0，不影响结果的正确性。

另外，\(a*b\) 和 \(\lfloor a * b \ / \ p \rfloor *p\) 可能很大，但是二者差一定是在 \([0, p-1]\) 之间的，我们只关心他们较低的若干位即可。

所以，我们用 long long 来保存 \(a*b\) 和 \(\lfloor a*b \ / \ p \rfloor\) 各自的结果。

如果整数运算溢出相当于舍弃高位，也正好符合我们的要求。

模意义下大整数乘法

64位整数乘法，题目链接：https://www.acwing.com/problem/content/92/

求 \(a\) 乘 \(b\) 对 \(p\) 取模的值，其中 \(1 \leq a, b, p \leq 10^{18}\)。

思路，把本来存进 long long 会炸掉的值先进行计算，用 long double 暂时存下，

然后再把差值，一个不会超过 long long 的数字塞回去

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

ll mul(ll a, ll b, ll p) {  
    a %= p, b %= p;
    ll c = (long double)a * b / p;
    ll ans = (a * b - c * p) % p;
    return ans < 0 ? ans + p : ans;
}

int main() {
    ll a, b, p;
    cin >> a >> b >> p;

    cout << mul(a, b, p) << '\n';

    return 0;
}

关于 long double

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int main() {
    double a = 3.14159265358979323846264338327950288419716939937510;
    long double b = 3.14159265358979323846264338327950288419716939937510L;

    cout.precision(50);

    cout << a << '\n';
    cout << b << '\n';
    cout << "3.14159265358979323846264338327950288419716939937510" << '\n';

    return 0;
}

image-20240702164615033

总结

快速乘——巧妙利用 long double，同样为了应对爆 long long

参考