欧拉函数

前置知识

算数基本定理（整数唯一分解定理），互质

目标

欧拉函数定义、证明、代码模板、性质、筛法求欧拉函数

定义

1 ~ N 中与 N 互质的数的个数被称为欧拉函数，记为 phi(N)

证明

代码模板

873. 欧拉函数

#include <bits/stdc++.h>

using namespace std;

int main() {
    int T;
    cin >> T;

    while (T--){
        int n;
        cin >> n;

        int res = n;
        for (int i = 2; i <= n / i; i++) {
            if (n % i == 0) {
                //res = res * (1 - 1 / i);
                res = res / i * (i - 1);
                while (n % i == 0) n /= i;
            }
        }
        if (n > 1) res = res / n * (n - 1);

        cout << res << endl;
    }

    return 0;
}

性质

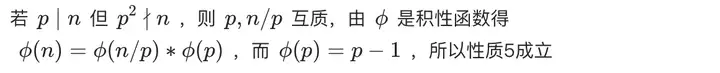
筛法求拉欧函数

// 埃式筛法，O(nlogn)
void euler(int n){
    for (int i = 2; i <= n; i++) phi[i] = i;
    for (int i = 2; i <= n; i++) 
        if (phi[i] == i)
            for (int j = i; j <= n; j += i)
                phi[j] = phi[j] / i * (i - 1); // 都乘上(1 - 1 / i)
}

// 线性筛法，O(n)
// 在线性筛法中，每个合数 n 只能被它的最小质因子 p 筛一次。
// 利用性质4、性质5，将phi(n / p) 递推到 phi(n)
int primes[110], phi[110], n;
int v[110]; // v[i]存i的最小质因子
int cnt;

void euler(int n){
    for (int i = 2; i <= n; i++) {
        if (v[i] == 0) { // i是质数
            v[i] = i, primes[cnt++] = i;
            phi[i] = i - 1;
        }

        // 给当前的数i，乘上一个质因子
        for (int j = 0; j < cnt; j++) {
            // i 有比 primes[j] 更小的质因子，或者超出 n 的范围，停止循环
            if (primes[j] > v[i] || primes[j] > n / i) break;

            // primes[j] 是合数 i * primes[j] 的最小质因子
            v[i * primes[j]] = primes[j];
            phi[i * primes[j]] = phi[i] * (i % primes[j] ? primes[j] - 1 : primes[j]);
            // primes[j]不整除i，性质5，phi(n) = phi(n / p) * (p - 1)
                        // primes[j]整除i，性质4，phi(n) = phi(n / p) * p
        }
    }
}

// 线性筛法，版本2，更简洁
void get_eulers(int n){
    phi[1] = 1;
    for (int i = 2; i <= n; i++){
        if (!st[i]){
            primes[cnt++] = i;
            phi[i] = i - 1;  //当i是质数的时候，i-1个数与i互质
        }

        for (int j = 0; primes[j] <= n / i; j++){
            st[primes[j] * i] = true;

            if (i % primes[j] == 0){
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }
}

题单

873. 欧拉函数

874. 筛法求欧拉函数

总结

欧拉函数定义、公式、证明、代码模板、性质、筛法求欧拉函数

参考

《算法进阶指南》