动态规划 01背包 完全背包 多重背包

前置知识

动态规划入门经典问题

目标

《背包九讲》中的基础部分，复杂的优化暂时不管

01背包

例题，01背包问题(含优化)

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];  // 右边集合为空，不包含i
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

// 滚动数组优化，f[N][M] -> f[2][M]

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[2][N];   
//计算f[i]这一层，只用到了f[i-1]这一层的数据，用滚动数组

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    f[0][0] = 0;
    for (int i= 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i & 1][j] = f[(i - 1) & 1][j];
            if (j >= v[i]) f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - v[i]] + w[i]);
        }

    cout << f[n & 1][m] << endl;

    return 0;
}

// 二维优化到一维

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];   

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);

            //这与我们的刚才的二维里的状态计算不一致，刚才实际应该是f[i - 1][j - v[i]]
            //若j从大到小枚举，算f[j]的时候，f[j - v[i]]还没有被更新过，存的就是f[i - 1][j - v[i]]
            //这样就和二维的状态转移方程等价了
        }

    cout << f[m] << endl;

    return 0;
}

// define ZerOnePack

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int f[N];
int v[N], w[N];

void zeroonepack(int f[], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        zeroonepack(f, v[i], w[i]);

    cout << f[m] << endl;

    return 0;
}

初始化的细节问题

完全背包问题

例题，完全背包问题(含优化)

// 3 loops
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    /*
    for 物品 枚举阶段
        for 体积 枚举状态
            for 决策 枚举决策
    */
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k *v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;

    return 0;
}

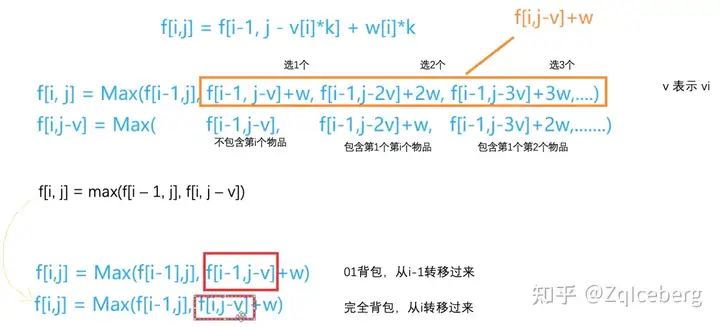
// 根据以上对转移方程的数学分析
// 3 loops -> 2 loops，减少了一层k循环

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

# 二维变成一维

求f[j]的时候，f[j–v[i]]已经被算过了， 
f[j-vi]是第i层的 f[j-vi] 和状态转移方程一致

// f[i][j] -> f[j]
// 二维变一维

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

想清楚： 一维的写法，为什么只差了从大到小循环 和 从小大到循环

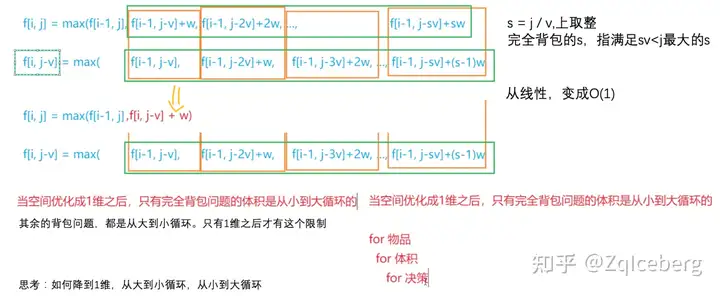
// define completepack

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        completepack(f, v[i], w[i]);

    cout << f[m] << endl;

    return 0;
}

多重背包问题

例题，多重背包问题 I

// 多重背包问题 I

// 0 < N,V ≤ 100
// 0 < vi,wi,si ≤ 100

// 3 loops
// O(n^3)

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;

    return 0;
}

// 另一种很直接的方法是
// 把第i种物品看做独立的Ci个物品，转化为∑Ci个物品的0/1背包问题

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int dp[N];
int v[N], w[N], s[N], n, V;

int main(){
    cin >> n >> V;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= s[i]; j++)
            for (int k = V; k >= v[i]; k--)
                dp[k] = max(dp[k], dp[k - v[i]] + w[i]);

    cout << dp[V] << '\n';

    return 0;
}

例题，多重背包问题 II

思路：0~7，可以恰好用几个 2的幂次 表示出来。

例如，0~7， 1+2¹⁺²2

但是，并不是所有的数字，都恰好。

例如，0~10，不能用 20, 21, 22, 23 。如果有 23 存在，可以表示的数字，就还有11, 12, 13, 14, 15了

所以，只能用 20, 21, 22 ，然后还有一个小尾巴 10−(1−23)=3 ，这样就可以表示 0~10 任意一个数了

// 多重背包问题 II
// O(Nlogs * V)
// 化简为O(NVlogs)

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000, M = 2010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)
        {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0)
        {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;

    for (int i = 1; i <= n; i++)     // 这个n是 原n*logs
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

// define multiplepack

#include <iostream>

using namespace std;

const int N = 1010, M = 2010;

int n, m;
int v[N], w[N], s[N];
int f[M];

void zeroonepack(int f[], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}

void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}

void multiplepack(int f[], int vi, int wi, int si)
{
    if (vi * si >= m){
        completepack(f, vi, wi);
        return ;
    }

    int k = 1;
    while (k < si){
        zeroonepack(f, k*vi, k*wi);
        si -= k;
        k *= 2;
    }
    if (si){
        zeroonepack(f, si*vi, si*wi);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> v[i] >> w[i] >> s[i];
        multiplepack(f, v[i], w[i], s[i]);
    }

    cout << f[m] << endl;

    return 0;
}

混合三种背包问题

01背包

def ZeroOnePack(F, C, W ) 
    for v = V to C
        F[v] = max(F[v],f[v − C] + W)

for i = 1 to N 
    ZeroOnePack(F, Ci, Wi)

完全背包

def CompletePack(F, C, W ) 
    for v = C to V
        F[v] = max{F[v],f[v − C] + W}

多重背包

def MultiplePack(F, C, W, M) 
    if C·M ≥ V
        CompletePack(F, C, W)
        return

    k := 1
    while k < M
        ZeroOnePack(kC, kW) M := M − k
        k := 2k
    ZeroOnePack(C·M, W·M)

01背包+完全背包的混合

for i = 1 to N
    if 第i件物品属于01背包
        for v = V to Ci
            F[v] = max(F[v],F[v − Ci] + Wi)
    else if 第i件物品属于完全背包
                for v = Ci to V
            F[v] = max(F[v],F[v − Ci] + Wi)

01背包+完全背包+多重背包的混合

for i = 1 to N
    if 第i件物品属于01背包
    ZeroOnePack(F ,Ci ,Wi ) 
    else if 第i件物品属于完全背包
    CompletePack(F ,Ci ,Wi )
    else if 第i件物品属于多重背包 
        MultiplePack(F ,Ci ,Wi ,Ni )

例题，混合背包问题

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        if (s == 0) //完全背包
        {
            for (int j = v; j <= m; j++) f[j] = max(f[j], f[j - v] + w);
        }
        else
        {
            if (s == -1) s = 1;
            for (int k = 1; k <= s; k *= 2)
            {
                for (int j = m; j >= k * v; j--)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;    
            }
            if (s)
            {
                for (int j = m; j >= s * v; j--)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }

    cout << f[m] << endl;

    return 0;
}



// 也可以存起来，再来一遍
#include <bits/stdc++.h>

using namespace std;

const int N = 40, M = 220, MM = 1e5 + 10;

int dp[N][M], w[N], v[N], s[N];
int V, n;
int f[MM], nw[MM], nv[MM], tot, knap[MM];

int main()
{
    cin >> V >> n;
    for (int i = 1; i <= n; i++){
        cin >> w[i] >> v[i] >> s[i];

        if (s[i] == 0){
            nw[++tot] = w[i]; nv[tot] = v[i];
            knap[tot] = 1;    //完全背包
        }
        else if (s[i] == 1){   //01背包
            nw[++tot] = w[i]; nv[tot] = v[i];
        }
        else{    //多重背包
            for (int j = 1; j <= s[i]; j = j << 1){
                s[i] -= j;
                nw[++tot] = w[i] * j; nv[tot] = v[i] * j;
            }
            if (s[i]){
                nw[++tot] = w[i] * s[i]; nv[tot] = v[i] * s[i];
                s[i] = 0;
            }
        }
    }

    for (int i = 1; i <= tot; i++){
        if (knap[i]){
            for (int j = nw[i]; j <= V; j++)
                f[j] = max(f[j], f[j - nw[i]] + nv[i]);
        }
        else{
            for (int j = V; j >= nw[i]; j--)
                f[j] = max(f[j], f[j - nw[i]] + nv[i]);
        }
    }

    cout << f[V] << '\n';

    return 0;
}

// define zeroonepack(),completepack(),multiplepack()

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N], s[N];
int f[N];

void zeroonepack(int f[], int vi, int wi)
{
    for (int j = m; j >= vi; j--)
        f[j] = max(f[j], f[j - vi] + wi);
}

void completepack(int f[], int vi, int wi)
{
    for (int j = vi; j <= m; j++)
        f[j] = max(f[j], f[j - vi] + wi);
}

void multiplepack(int f[], int vi, int wi, int si)
{
    if (vi * si >= m){
        completepack(f, vi, wi);
        return ;
    }

    int k = 1;
    while (k < si){
        zeroonepack(f, k*vi, k*wi);
        si -= k;
        k *= 2;
    }
    if (si){
        zeroonepack(f, si*vi, si*wi);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> v[i] >> w[i] >> s[i];

        if (s[i] == -1) zeroonepack(f, v[i], w[i]);
        else if (s[i] == 0) completepack(f, v[i], w[i]);
        else multiplepack(f, v[i], w[i], s[i]);
    }

    cout << f[m] << endl;

    return 0;
}

总结

01背包，要注意一维的写法，循环的顺序

初始化的细节问题，可以引起很多基础问题的理解

完全背包，要注意一维的写法，为什么从前往后循环

多重背包，要注意，还有倍增和单调队列的优化

混合三种背包问题，是对上述代码的综合应用，考察对定义的理解和代码能力

参考

背包九讲-崔天翼-2.0

AcWing