动态规划 经典问题入门¶
前置知识¶
递推、递归、搜索、贪心
目标¶
数字三角形问题
最长上升子序列问题
最长公共子序列问题
最大子段和问题
1、数字三角形问题¶
有一些数字排成数塔的形状,
其中第一层有一个数字,第二层有两个数字,……,第n层有n个数字。
现在要从第一层走到第n层,每次只能选择左下方或者右下方的数字,
问:“最后将路径上所有数字相加后得到的和最大是多少?”
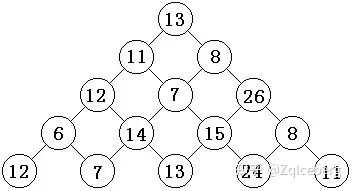
引导思考:
(1)从起点到第一行第一列的答案是固定的。
(2)在第一步骤基础上,从起点到第二行的答案也是固定的。
(3)走到第3行第2列的 数字7 时,有两种选择,显然会选择从累积更大的过来才是最优的
若将f[i][j]定义为从第一行第一列到第 i 行第 j 列的路径上的数字和的最大值,
则到 数字7 的递推式为:f[3][2] = max(f[2][1],f[2][2]) + 7
(4)可得出一般递推式为 f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j]
我们只需要推到第n行,就可以得到ans = max{f[n][1…n]}
解法提炼:
(1)状态定义:
f[i][j]定义从第一行第一列到第 i 行第 j 列的路径上的数字和的最大值
(2)所求:
max{f[n][1…n]}
(3)状态转移:
f[i][j]=max(f[i-1][j-1],f[i-1][j]) + a[i][j]
示范代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int a[N][N], dp[N][N], n;
int main(){
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++) cin >> a[i][j];
memset(dp, -0x3f, sizeof dp);
dp[1][1] = a[1][1];
for (int i = 2; i <= n; i++) // 从第二行开始具有推导关系
for (int j = 1; j <= i; j++){
dp[i][j] = max(dp[i][j], dp[i - 1][j] + a[i][j]);
if (j > 1) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + a[i][j]);
}
// 在最后一行,进行打擂台,维护答案
int ret = -2e9;
for (int j = 1; j <= n; j++) ret = max(ret, dp[n][j]);
cout << ret << '\n';
return 0;
}
2、最长上升子序列问题¶
给定一个长度为 n 的数字序列,求最长的上升子序列长度。
如 3、1、2、6、4、5 的最长上升子序列
为 1、2、4、5,故答案为 4。
解法提炼
(1)状态定义:
f[i] 定义为到第 i 个数字为止,
且第 i 个数必须为该子序列的最后一个数字时,所获得的最长子序列的长度。
(2)所求:
max{f[1…n]}
(3)状态转移:
f[i] = max{f[j] + 1} | 1 <= j <= i-1, a[j] < a[i]。
示范代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N], dp[N], n;
int main()
{
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++){
dp[i] = 1;
for (int j = 1; j < i; j++)
if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i++) res = max(res, dp[i]);
cout << res << '\n';
return 0;
}
3、最长公共子序列问题¶
给定两个长度为 n 的数字序列,求最长的公共子序列长度。
第一个数字序列为 1、6、2、5、4、7,
第二个数字序列为 1、2、5、5、2、7,
则最长的公共子序列为1、2、5、7,其长度为4。
解法提炼
(1)状态定义:
f[i][j] 定义为当第一行数字取到第 i 个,第二行数字取到第 j 个时,
所能得到的最长子序列长度,
且第 i 个数字和第 j 个数字不需要为所求子序列的最后一个数字(即这两个数字取到与否都可以)
(2)目标:
f[n][n]
(3)状态转移:
f[i][j] = f[i-1][j-1] + 1 | a[i] = b[j]
max(f[i-1][j], f[i][j-1]) | a[i] ≠ b[j]
当 a[i] 与 b[j] 相等时,其会对目标值贡献 +1,
而 a[i] 与 b[j] 不相等时,显然这两个数字无法配对,
对 f[i][j] 而言,a[i] 和 b[j] 中必有一个是多余的,
因此,f[i][j] = max(f[i-1][j], f[i][j-1])
此时计算 f[i][j] 的时间复杂度为 O(1),总的时间复杂度为 O(n^2)。
4、最大子段和问题¶
Given an array of n numbers, our task is to calculate the maximum subarray sum.
举例
-1 2 4 -3 5 2 -5 2
最大子段和是10
2 4 -3 5 2
解法提炼
首先我们明确一下 dp[i] 代表什么
dp[i] 代表以第 i 个元素为结尾的最大子段和的长度
注意,这里的表达,有一个细节
这个子段,可以是 ...i,也可以是 i
可以是接在前面的猴屁股上的,也可以是自己就是一个子段
为什么?
如果 dp[i-1] 是一个负数,那么接在 i-1 的后面,肯定不如自己干合适。
示范代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N], n;
int ret = -2e9;
int dp[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
dp[i] = max(a[i], dp[i - 1] + a[i]);
ret = max(ret, dp[i]);
}
cout << ret << '\n';
return 0;
}
题单¶
总结¶
动态规划是一个分水岭,很自然的就会认为这东西不好学,难倒了很多人
先从经典例题入手,模仿,照搬,照抄,这些方法统统用上,不必考虑什么创新,甚至什么理解
当这几个经典例题很流利的情况下,我们再进去理解动态规划的原理、专业术语
简单来讲,先学下去,再说