DFS¶
前置知识¶
递归
目标¶
深度优先搜索模板题,尝试理解“状态”这个概念。
What¶
● 搜索,又称状态空间搜索,是指通过搜索从初始状态到目标状态的路径以完成问题求解的算法。
● depth first search(dfs), 按照深度优先的顺序对“问题状态空间”进行搜索的算法(理解理解搜索树,是不是深度优先?)。
● “深搜”,是一种包括遍历形式、状态记录与检索、剪枝优化等算法整体设计的统称。提前学习建图方法后,掌握在图上进行遍历,进一步把“问题空间”类比为一张图。
● 研究dfs算法之前,要定义该过程产生的 “搜索树” 结构,整个深搜算法就是基于该搜索树完成的(用递归实现的指数型枚举、排列性枚举、组合型枚举,其实就是深搜的三种最简单的形式)。
● dfs,常常指利用递归函数实现暴力枚举的算法。
● 递归搜索,该类搜索算法的特点在于,将要搜索的目标分成若干“层”,每层基于前几层的状态进行决策,直到达到目标状态。
How¶

八皇后问题
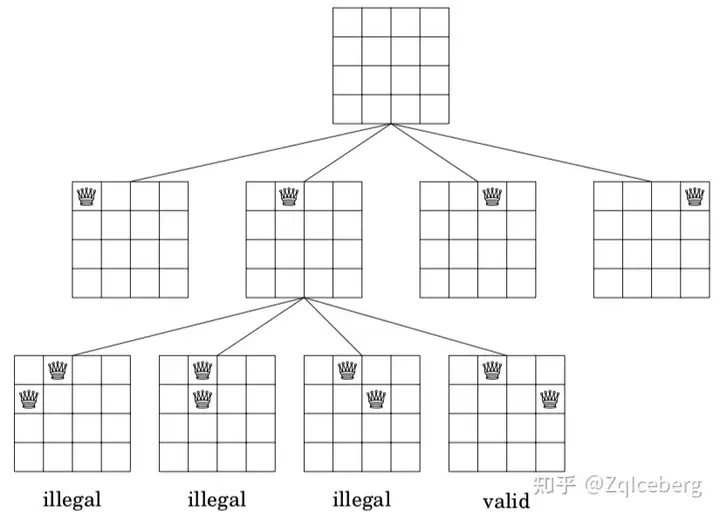
上图是,四皇后,递归搜索树,示例
// n皇后代码模板
// 按行枚举
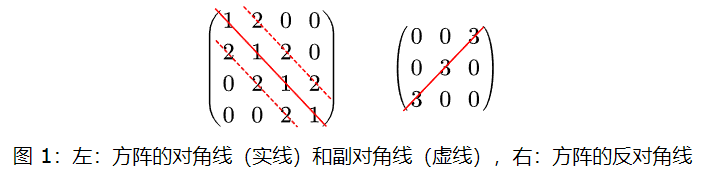
//(1)反对角线 y=x+b, 截距 b=y−x,因为我们要把 b 当做数组下标,所以 b 不能是负的
// 所以我们 +n,保证是结果是正的
//(2)而对角线 y=−x+b, 截距是 b=y+x,这里截距一定是正的,所以不需要加偏移量
// 反对角线,左上到右下
// 对角线,左下到右上
// 反对角线udg[n−u+i],对角线 dg[u+i]中的下标
// n−u+i,u+i 表示的是截距
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u)
{
// u == n 表示已经搜了n行,故输出这条路径
if (u == n)
{
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
//剪枝(对于不满足要求的点,不再继续往下搜索)
//udg[n - u + i],+n是为了保证大于0
if (!col[i] && !dg[u + i] && !udg[n - u + i])
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
// 恢复现场 这步很关键
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
代码框架
题单¶
总结¶
DFS 是一个非常重要的基础算法,虽然基础,但可以用到最后的算法。
其难度,随着题面逻辑的复杂而提升,抽象的问题定义,将会成为难点。
俗话说的好,“暴力拿省一”,甚至,暴力拿金牌。虽然都是暴力,但是人家的暴力,可是高级的暴力。
一个题目,人家说,暴力,可能你连题目说的是什么,都无法有效的阅读理解。
在普及组阶段,应该不贪多,学到了 DFS,就做一个阵地战,把 DFS 打死打穿,就不往后面走了。直接去参加比赛,也依然没有大问题,甚至表现还要优于贪多的选手。
打磨技能的这个过程中,我们将获得基础能力的积累和提升,为后续算法的有效推进,做好准备。
参考¶
《信息学奥林匹克辞典》