Catalan数¶
这是一个教学篇。
前置知识¶
组合数的计算
目标¶
Catalan数的典型示例
Catalan数的计算公式
Catalan数的证明过程
Catalan数,是什么¶
Catalan数 \(C_n\),等价于 由 n 个左括号和 n 个右括号组成的合法的括号表达式数。
什么样的括号表达式,是合法的:
- 一个空的括号表达式,是合法的
- 如果 \(A\) 合法,那么 \((A)\) 合法
- 如果 \(A\) 和 \(B\) 合法,那么 \(AB\) 合法
换一种表达方式
什么样的括号表达式,是合法的:
- 括号表达式的任意前缀,左括号的数量要大于等于右括号的数量
- 整个括号表达式中,左括号的数量等于右括号的数量
Catalan数,公式一¶
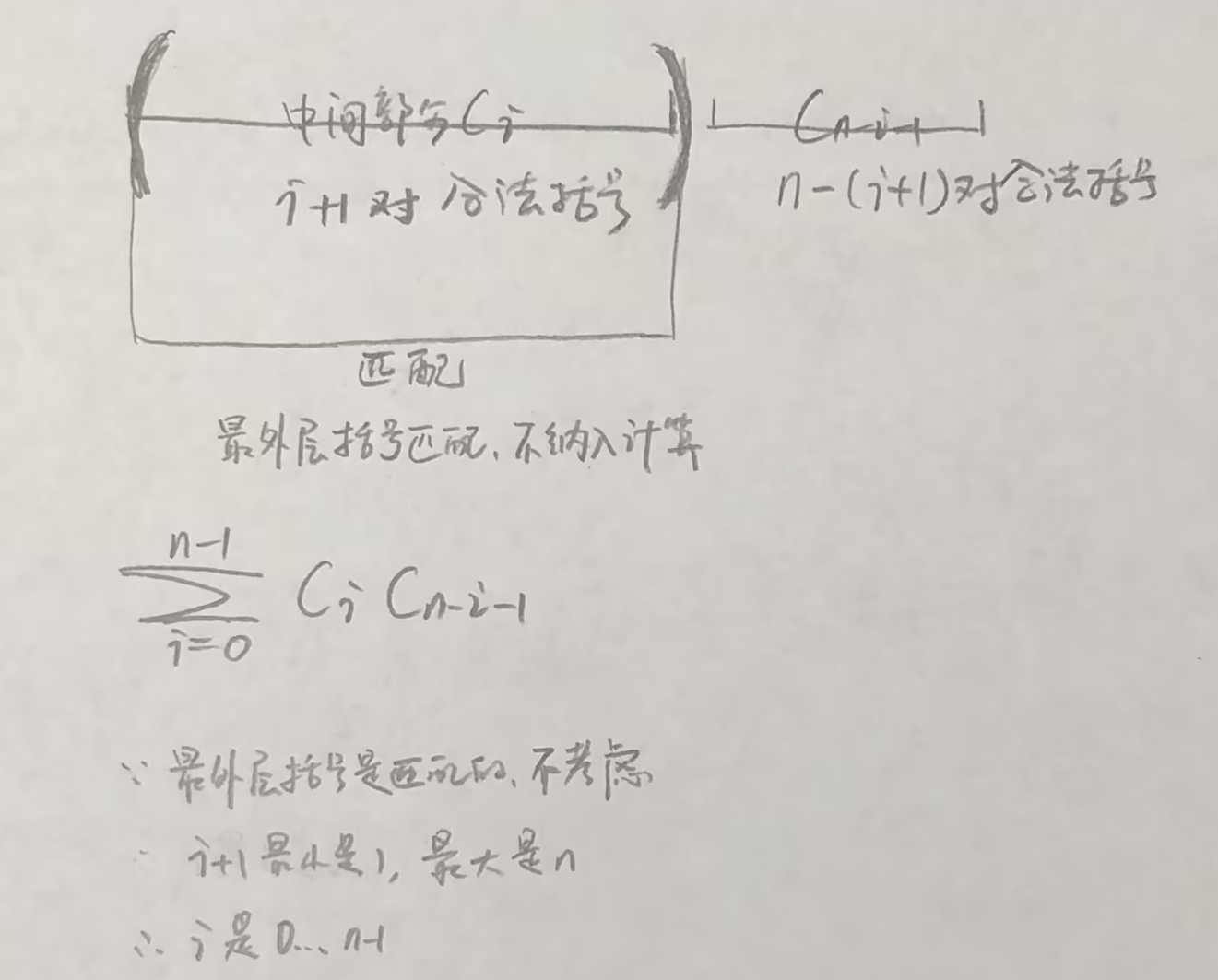
结合上图分析,我们将表达式分成两部分,两部分都是合法的括号表达式,左半部分尽可能短,但非空。例如,左半部分包含了 i+1 对合法的括号(+1,是指左半部分最外层的那对括号)
- \(C_i\) 是指,不计算最外层匹配的那对括号,合法括号表达式数
- \(C_{n-i-1}\)是指,右半部分的合法括号表达式数
初始条件 \(C_0 = 1\),我们可以用0对括号构造出一个合法的括号表达式,即空的表达式。
我们也可以从二叉树的视角,来看这个证明过程。
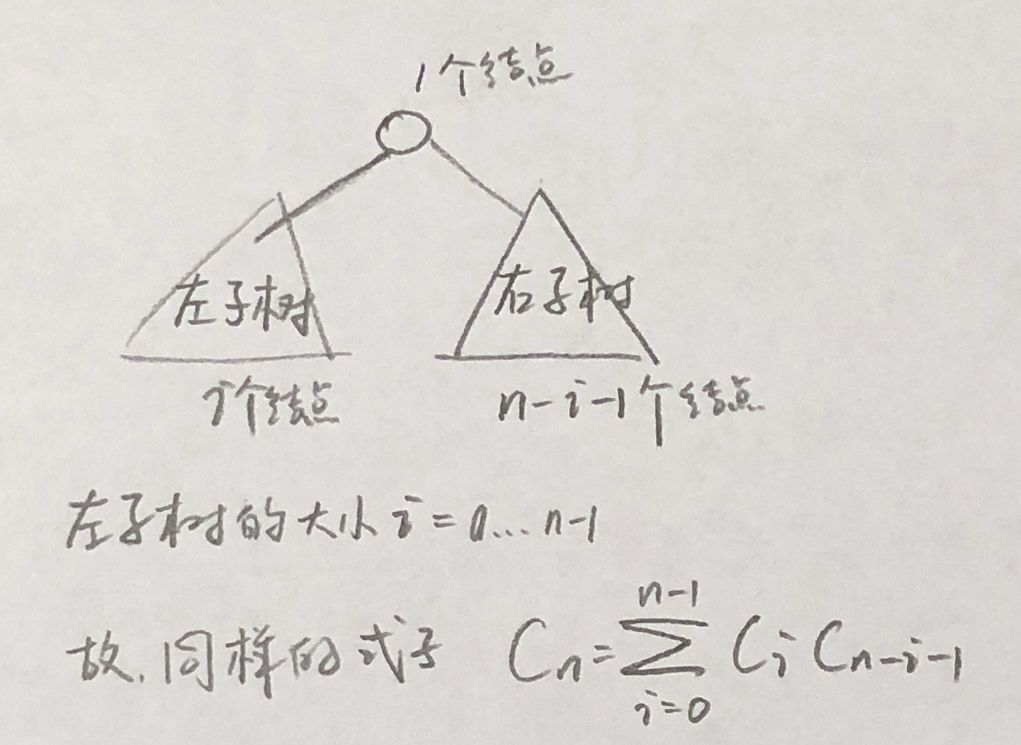
Catalan数,公式二¶
我们从括号表达式这个问题,看这个公式的证明。我们还是用 \(2n \choose n\) 表示n个左括号和n个右括号组成的括号表达式的方案数,但不一定是合法的。
如果一个括号表示式是非法的,那么它包含了一个前缀,这个前缀中右括号的数量比左括号的数量多。
我们把这个前缀中的括号,进行变换,左括号变右括号,右括号变左括号。例如,())()( 包含了一个前缀 ())(右括号比左括号多),变换之后是 )((()(。
这样变换完毕之后,整个括号表达式就包含了 n+1 个左括号和 n-1 个右括号,此时括号表达式的方案数是 \(2n \choose {n}\),这刚好代表了非法的方案数。因此,我们用 总方案数 - 非法方案数 = 合法方案数。 $$ C_n = {2n \choose n} - {2n \choose n+1} = {2n \choose n} - \frac{n}{n+1}{2n \choose n}= \frac{1}{n+1}{2n \choose n} $$
我们也可以从进栈出栈的视角,来看这个证明过程。
一个栈(无穷大)的进栈序列为 1, 2, 3, ..., n 有多少个不同的出栈序列?
令 1 表示进栈,0 表示出栈,则可转化为求一个 2n 位、含 n 个 1、n 个 0 的二进制数,满足从左往右扫描到任意一位时,经过的 0 数不多于 1 数。
显然含 n 个 1、n 个 0 的 2n 位二进制数共有 \(2n \choose n\) 个,下面考虑不满足要求的数目。
考虑一个含 n 个 1、n 个 0 的 2n 位二进制数,扫描到第 2m+1 位上时,有 m+1个 0 和 m 个 1(容易证明一定存在这样的情况),后面的 01排列中,必然有 n-m 个 1, n-m-1个0。
将 2m+2 位置及其以后的部分,0 变成 1,1 变成 0,则整个数列变成了一个 n+1 个 0 和 n-1 个 1 的二进制数。反之亦然。
一个含有 n+1 个 0 和 n-1 个 1 的二进制数共有 \(2n \choose n+1\) 个。
从而 \(C_n = {2n \choose n} - {2n \choose n+1} = {2n \choose n} - \frac{n}{n+1}{2n \choose n}= \frac{1}{n+1}{2n \choose n}\),用整体的方案数,减去非法的方案数,剩下的就是合法方案数。
证毕。
注释:
\({2n \choose {n+1}} = \frac {(2n)!}{(2n-n-1)!(n+1)!} = \frac {(2n)!}{(n-1)!(n+1)!}\)
\({2n \choose n} = \frac {(2n)!}{(2n-n)!n!} = \frac {(2n)!}{n!n!}\)
\(\therefore {2n \choose {n+1}} = \frac{n}{n+1}{2n \choose n}\)
Catalan数,能解决什么问题¶
长度 2n 的 Dyck 词的个数,Dyck 词是一个有 n 个 X 和 n 个 Y 组成的字符串,且所有的前缀子串皆满足 X 的个数大于等于 Y 的个数。以下为长度是 6 的 Dyck 词:XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
长度 2n 的 合法括号运算式的个数。((())) ()(()) ()()() (())() (()())
n 个结点可构造多少个不同的二叉树?下图中,n等于3,圆形表示节点,月牙形表示什么都没有。

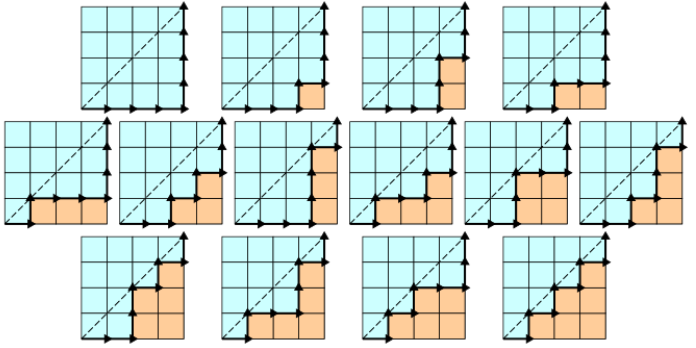
有一个大小为 n*n 的方格图左下角为 (0, 0) 右上角为 (n, n),从左下角开始每次都只能向右或者向上走一单位,不走到对角线 y = x 上方(但可以触碰)的情况下到达右上角有多少可能的路径?计算这种路径的个数等价于计算Dyck 词的个数:X代表“向右”,Y代表“向上”。下图为 n = 4 的情况:
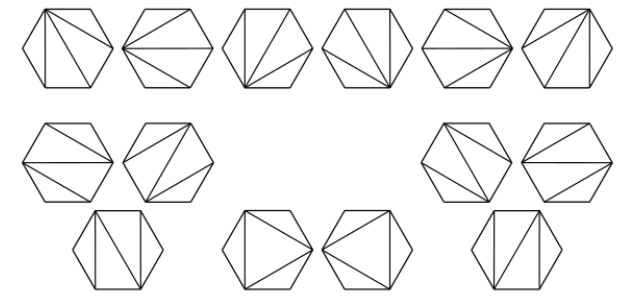
对角线不相交的情况下,将一个 n + 2 边的凸多边形区域分成三角形区域的方法数?下图为 n = 4 的情况:
有 2n 个人排成一行进入剧场。入场费 5 元。其中只有 n 个人有一张 5 元钞票,另外 n 人只有 10 元钞票,剧院无其它钞票,问有多少种方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?
一个栈(无穷大)的进栈序列为 1, 2, 3, ..., n 有多少个不同的出栈序列?
由 n 个 \(+1\) 和 n 个 \(-1\) 组成的 2n 个数 \(a_1, a_2, ...,a_{2n}\),其部分和满足 \(a_1 +a_2+...+a_k \geq 0(k=1,2,...,2n)\),有多少个满足条件的数列?
在圆上选择 2n 个点,将这些点成对连接起来使得所得到的 n 条线段不相交的方法数?
用 n 个长方形填充一个高度为 n 的阶梯状图形的方法个数。下图为 n = 4 的情况:

参考¶
https://oi-wiki.org/math/combinatorics/catalan/卡特兰数
https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0卡特兰数
https://en.wikipedia.org/wiki/Catalan_number Catalan number