二叉搜索树 BST¶
前置知识¶
二叉树,堆
目标¶
掌握模板代码
What¶
给定一颗二叉树,树上的每个结点都带有一个数值,称为结点的“关键码”。对于树中的任意一个结点:
- 该结点的关键码不小于它的左子树中的任意结点的关键码
- 该结点的关键码不大于它的右子树中的任意结点的关键码
满足上述性质的二叉树,就是一棵“二叉查找树”(Binary Search Tree, BST)。
显然,二叉查找树的中序遍历,是一个关键码单调递增的结点序列。
BST 的建立¶
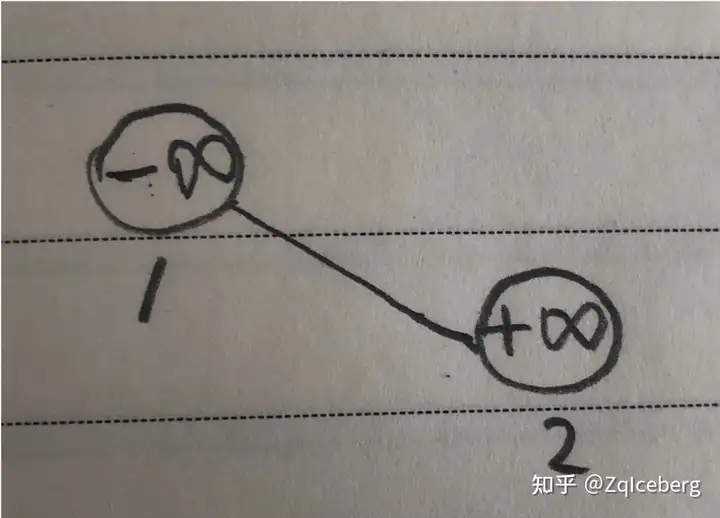
为了避免越界、减少边界情况的特判,在 BST 中额外插入两个结点,一个关键码无穷大,一个关键码无穷小。
假设,BST 中不会含有关键码相同的结点。
struct BST {
int l, r;
int val;
}a[N]; // 模拟数字链表
int tot, root, INF = 1 << 30;
int New(int val) {
a[++tot].val = val;
return tot;
}
void Build() {
New(-INF), New(INF);
root = 1, a[1].r = 2; // 结点1,无穷小;结点2,无穷大
}
BST 的检索¶
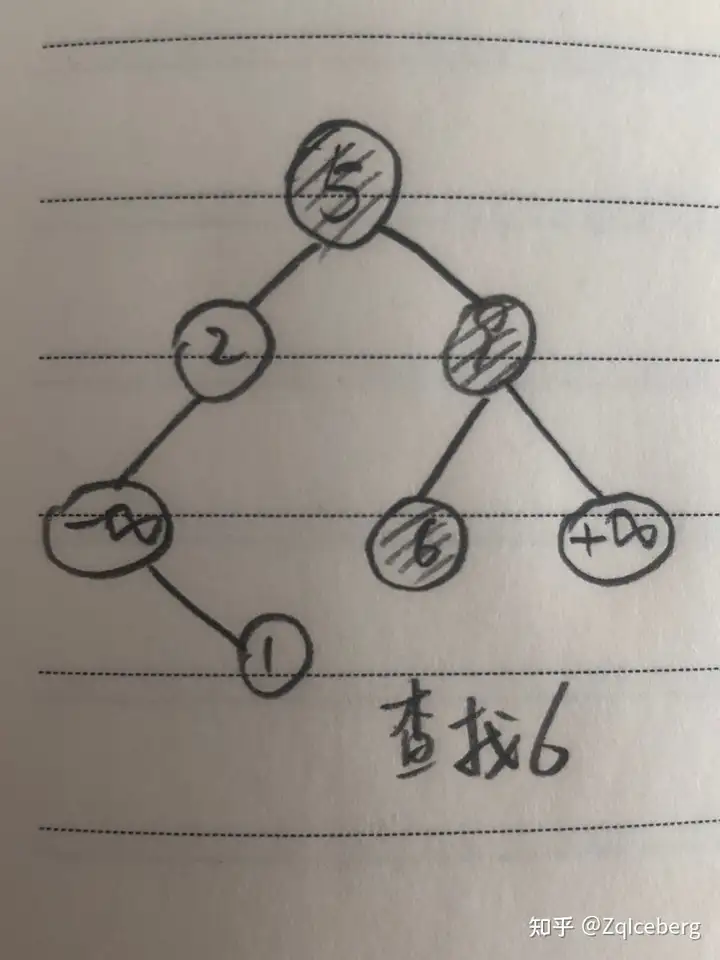
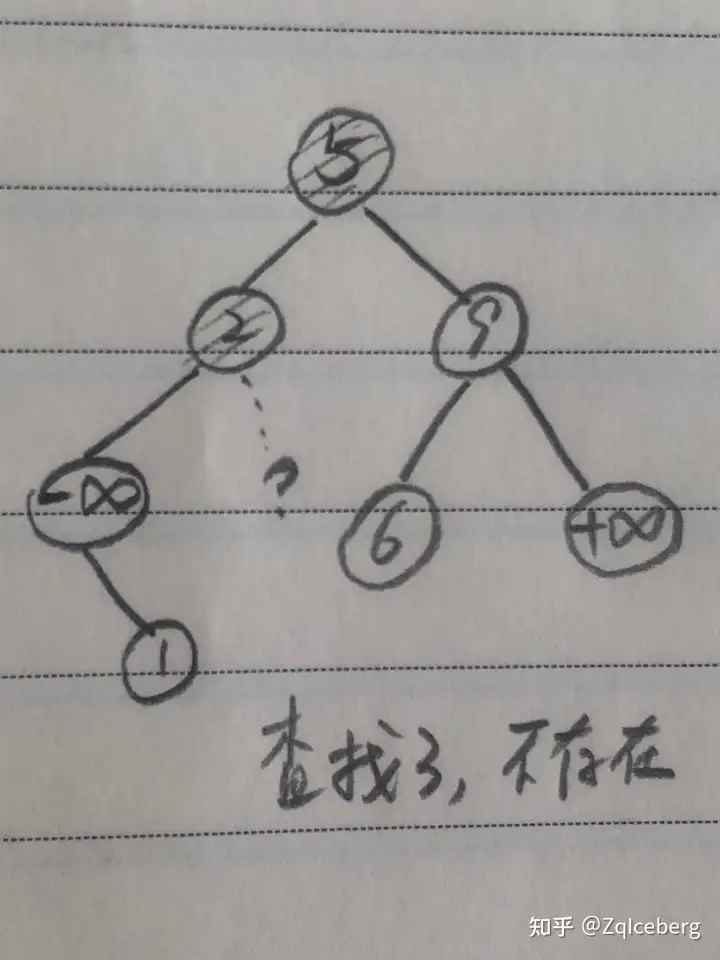
在 BST 中检索是否存在关键码为 val 的结点
int Get(int p, int val) {
if (p == 0) return 0; // 没找到
if (val == a[p].val) reutrn p; // 找到了
return val < a[p].val ? Get(a[p].l, val) : Get(a[p].r, val);
}
// 调用的时候,令变量p 等于根结点root
// Get(root, val);
BST 的插入¶
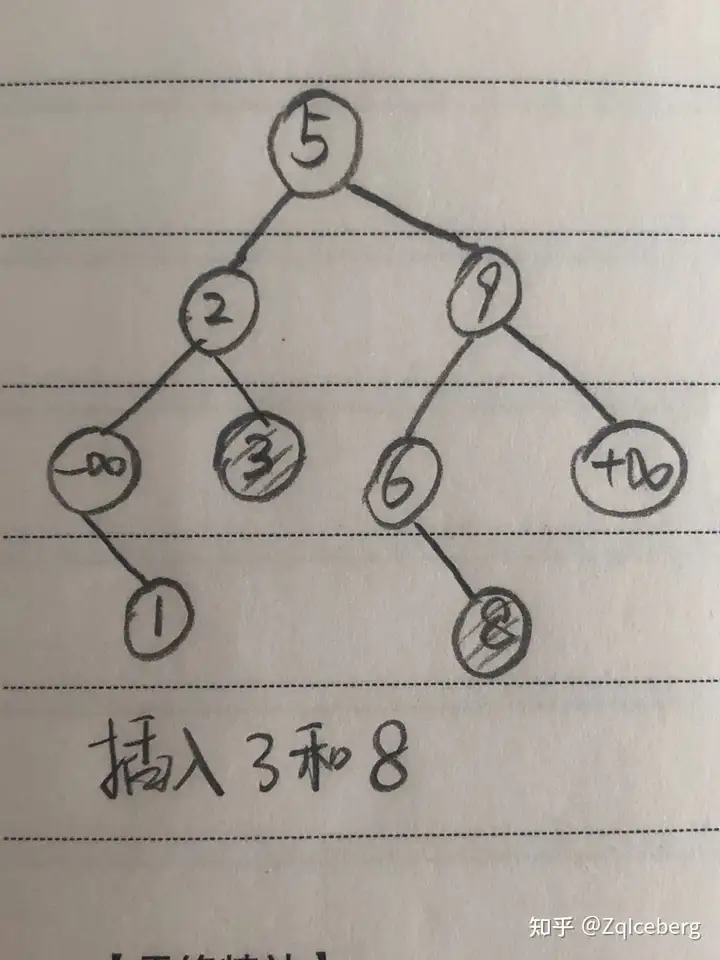
在 BST 中插入一个新的值 val(假设,之前不存在关键码 val)
这个过程与检索过程类似。当发现要走向的结点 p 的子结点为空,说明 val 不存在。
直接建立关键码为 val 的新节点,作为 p 的子结点。
void Insert(int &p, int val) {
if (p == 0) {
p = New(val); // 其父亲节点的 l 或 r 会被同时更新
return ;
}
if (val == a[p].val) return ;
if (val < a[p].val) Insert(a[p].l, val);
else Insert(a[p].r, val);
}
BST 求前驱/后继¶
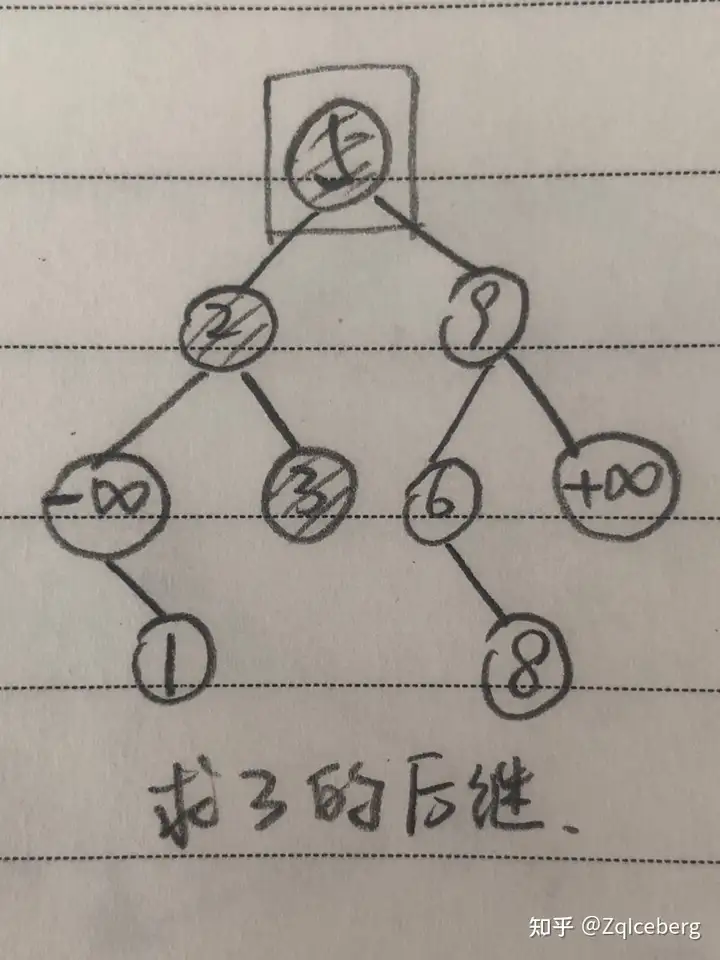
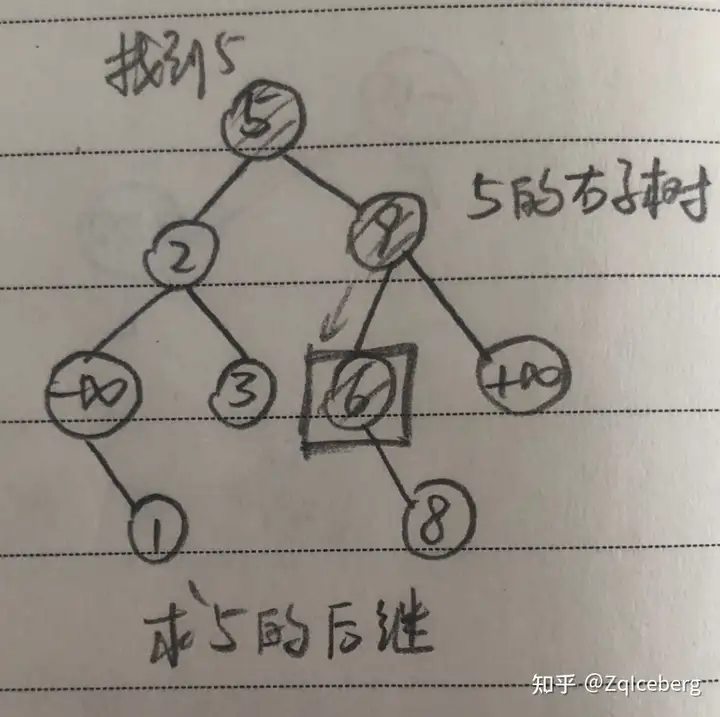
以求后继为例,val 的后继是指,在 BST 中关键码大于 val 的最小的那个节点。
令后继 ans 为无穷大,然后在 BST 中检索 val,每经过一个结点,都检查该结点的关键码,判断能否更新所求的后继 ans。
int GetNext(int val) {
int ans = 2; // 结点2,无穷大
int p = root;
while (p) {
if (val == a[p].val) {
if (a[p].r > 0) { // 有右子树
p = a[p].r;
// 在右子树上一直向左走
while (a[p].l > 0) p = a[p].l;
ans = p;
}
break;
}
// 每经过一个结点,都尝试更新后继
if (a[p].val > val && a[p].val < a[ans].val) ans = p; // 后继,是指大于val的结点中,最小的
p = val < a[p].val ? a[p].l : a[p].r;
}
return ans;
}
BST 的结点删除¶
首先,在 BST 中,找到关键码为 val 的结点 p。
若 p 的子结点个数小于 2,则直接删除 p,并令 p 的子结点代替 p 的位置,与 p 的父节点相连。
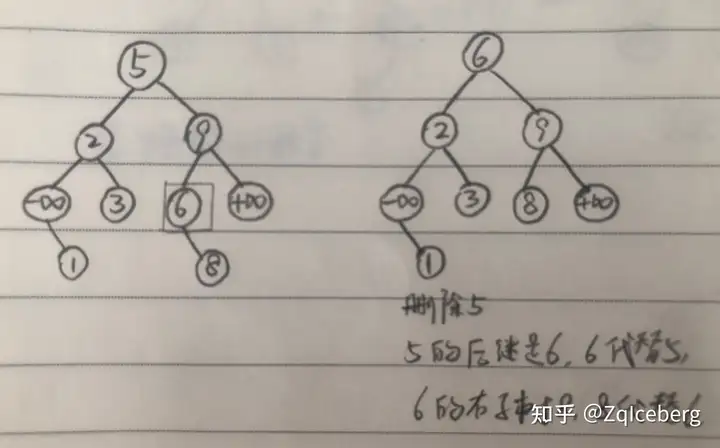
如 p 既有左子树,又有右子树,则先找到 p 的后继结点 next。
因为 next 是没有左子树的,所以可以直接删除 next,并令 next 的右子树代替 next 的位置。
最后,让 next 代替 p,删除 p。
void Remove(int &p, int val) {
if (p == 0) return ;
if (val == a[p].val) {
if (a[p].l == 0) p = a[p].r; // 子结点个数小于2,直接用子结点替换p
else if (a[p].r == 0) p = a[p].l;
else { // 既有左子树,又有右子树
int next = a[p].r; // 求后继结点next
while (a[next].l > 0) next = a[next].l;
Remove(a[p].r, a[next].val); // 后继结点是没有左子树的,如果有,就要继续下放了
a[next].l = a[p].l, a[next].r = a[p].r; // 挂载好左儿子、右儿子
p = next; // 再赋值过去,此处p是引用
}
return ;
}
if (val < a[p].val) Remove(a[p].l, val);
else Remove(a[p].r, val);
}
总结¶
在随机数据中,BST 一次操作的期望复杂度为 O(logn)。然而,BST 很容易退化。
例如,在 BST 中依次插入一个有序序列,将会得到一个链,平均每次操作的复杂度为 O(n)。
当左右子树相差很大时,BST 是“不平衡的”。
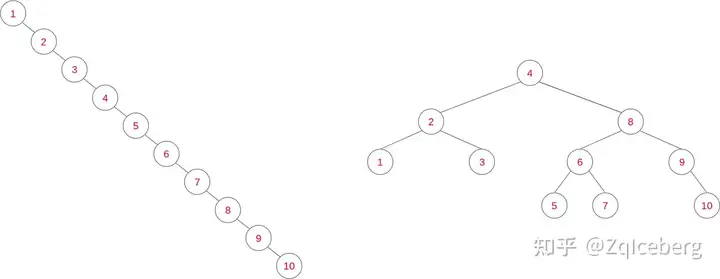
It’s easy to see that the order of insertions in the BST will affect the height of the tree. In the left figure (worst case scenario), we inserted elements from 1 to 10 sequentially. In the right figure (best case scenario) we inserted the elements 4, 8, 2, 3, 6, 9, 5, 7, 1, 10
参考¶
《算法竞赛进阶指南》