原码、反码、补码¶
为什么使用原码、反码、补码¶

原码¶
原码 (True form,未经更改的码) 就是用第一位表示符号,其余位表示值。比如如果是8位二进制:

反码¶
正数的反码是其本身
负数的反码是在其原码的基础上,符号位不变,其余各个位取反
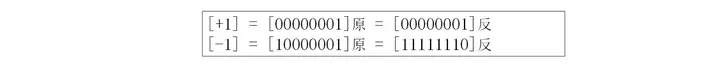
补码¶
正数的补码就是其本身
负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1。即在反码的基础上+1
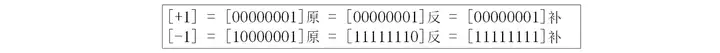
补码(英语:2's complement)是一种用二进制表示有符号数的方法,也是一种将数字的正负号变号的方式,常在计算机科学中使用。补码以有符号比特的二进制数定义。
正数和0的补码就是该数字本身再补上最高比特0。负数的补码则是将其绝对值按位取反再加1。
补码有什么用¶
补码系统的最大优点是可以在加法或减法处理中,不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有号数加法,而且减法可以用一个数加上另一个数的补码来表示,因此只要有加法电路及补码电路即可完成各种有号数加法及减法,在电路设计上相当方便。
举例,8-bit补码系统的整数¶
下表是一些 8-bit 补码系统的整数。它的可表示的范围包括 -128 到 127,总共 256(\(2^8\))个整数。
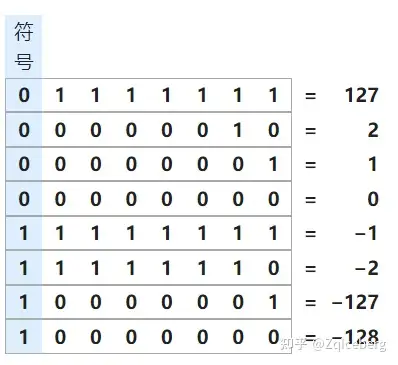
另外,补码系统的0就只有一个表示方式,这和反码系统不同(在反码系统中,0 有二种表示方式),因此在判断数字是否为 0 时,只要比较一次即可。
举例,4位的补码数字,进行加法运算¶
以下用4位的补码数字来说明补码系统的数字表示方式。
- 在表示正数和零时,补码数字和一般二进制一样,唯一的不同是在补码系统中,正数的最高比特恒为 0,因此 4 位的补码正数,最大数字为 0111 (7)。
- 补码数字的负数,最高比特恒为 1,4 位补码的数字中,最接近 0 的负数为 1111 (-1),以此类推,因此绝对值最大的负数是 1000 (-8)。
以上的表示方式在电脑处理时格外方便,用以下的例子说明:
结果 10010 似乎是错的,因为已经超过四个比特,不过若忽略掉(从右开始数)第 5 个比特,结果是 0010 (2),和我们计算的结果一样。而且若可以将二进制的 1111 (-1) 变号为 0001 (1),以上的式子也可以计算减法:\(3 - 1 = 2\)。(关键词:溢出overflow)
举例,计算补码¶
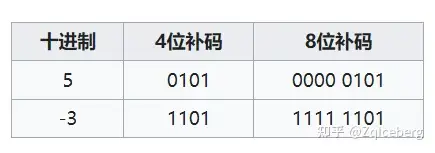
有符号位8位二进制表示的数字5:
0000 0101 (5)
其最高比特为0,因为此数字为正数。若要用补码系统表示 -5,首先要将5的二进制进行反相运算〔1变为0,0变为1 〕:
1111 1010
目前的数字是数字5的反码,因此需要再加1,才是补码:
1111 1011 (-5)
以上就是在补码系统中 -5的表示方式。其最高比特为1,因为此数字确实为负数。
一个负数的补码就是其对应的正数。以 -5为例,先求数字的反码:
0000 0100
再加一就是 -5的补码,也就是5。
0000 0101 (5)
简单来说,数字a(正负数皆可)的补码即为 -a。
举例,特别的数字0与-128¶
0的补码计算方式(以8位为例)如下:先计算它的反码:
1111 1111
再将反码加一:
0000 0000,溢出比特二进制值 = 1(二进制)
忽略溢出,其结果为0(0是唯一计算补码过程中会出现溢出的数字。)。
因此0的补码为0。
而0 x (-1) = 0,因此其补码仍满足“数字a的补码为 -a”的原则。
若计算1000 0000(这是8位内可表示有符号位区分的二进制形式的最大负数-128)的补码:先计算它的反码:
0111 1111
再加一就是它的补码。
1000 0000
1000 0000 (-128)的补码仍为1000 0000 (-128)。但(-128) x (-1) = 128,因此其补码是以上规则的例外。
总结:由于0可以等于0的补码-0,以及同样因为8位的补码可显示的值范围为 -128 ~ 127,
但-128的补码128无法用在已有比特数量为8的比特数量内的可用补码表示。
在计算其他位数内的可表示有符号位区分的二进制形式的最大负数(即1000...000)时,也会有类似情形。
所以:0和-128的确是“数字a的补码为 -a”原则中两个特别的数字。
补码的工作原理¶
为什么补码能这么巧妙实现了正负数的加减运算?答案是:指定 n 比特字长,那么就只有 \(2^n\) 个可能的值,加减法运算都存在上溢出与下溢出的情况,实际上都等价于模 \(2^n\) 的加减法运算。
例如,8位无符号整数的值的范围是0到255.因此4+254将上溢出,结果是2,即
(4 + 254) mod 256 = 258 mod 256 = 2
例如,8位有符号整数的值的范围,如果规定为−128到127,则126+125将上溢出,结果是−5,即
(126 + 125) mod 256 = 251 mod 256 = -5
符号延展¶
将一个特定比特补码系统的数字要以较多比特表示时(例如,将一个字节的变量复制到另一个二个字节),所有增加的高比特都要填入原数字的符号比特。在一些微处理机中,有指令可以执行上述的动作。若是没有,需要自行在程序中处理。
在补码系统中,当数字要向右位移几个比特时,在位移后需将符号比特再填入原位置(算术移位),保持符号比特不变。以下是两个例子:
而当一个数字要向左位移 n 个比特时,最低比特填 n 个0,权值最高的 n 个位被抛弃。以下是两个例子:
向右位移一次相当于除以2,利用算术移位的方式可以确保位移后的数字正负号和原数字相同,因为一数字除以 2 后,不会改变其正负号。
注意:向左位移一次相当于乘以 2,虽然乘以在理论上并不会改变一个数的符号,但是在补码系统中,用以表示数的二进制码长度有限,能够表示的数的范围也是有限的:若一个数的高权值上的数位已经被占用,此时再将这个数左移若干位(乘以 \(2^n\))的话,有可能造成数位溢出(overflow),高权值上的数将会失去,对于绝对值很大数,这将造成整体表达的错误。
总结¶
原码
反码
补码,负数的补码是,按位取反,加 1。
知道一个负数的二进制,求对应的十进制。拿掉符号位,依然是,按位取反,加 1。
符号延展,补什么数字